题目内容
已知二次函数f(x)＝ax2－(a＋2)x＋1(a∈Z)，且函数f(x)在(－2，－1)上恰有一个零点，则不等式f(x)>1的解集为( )
A．(－∞，－1)∪(0，＋∞) B．(－∞，0)∪(1，＋∞)
C．(－1,0) D．(0,1)
C
[解析] ∵f(x)＝ax2－(a＋2)x＋1，Δ＝(a＋2)2－4a＝a2＋4>0，
∴函数f(x)＝ax2－(a＋2)x＋1必有两个不同的零点，
又f(x)在(－2，－1)上有一个零点，
则f(－2)f(－1)<0，
∴(6a＋5)(2a＋3)<0，
∴－
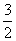<a<－
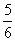，又a∈Z，
∴a＝－1，不等式f(x)>1即为－x2－x>0，解得－1<x<0.
练习册系列答案
相关题目
，那么a12＝________.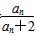
(n∈N*)．若bn＋1＝(n－λ)(
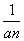＋1)(n∈N*)，b1＝－λ，且数列{bn}是单调递增数列，则实数λ的取值范围为( )
＋a＋b(a、b为正实数)，若1⊙k<3，则k的取值范围为________．
(k∈N*)．已知一个铁钉受击3次后全部进入木板，且第1次受击后进入木板部分的铁钉长度是铁钉长的
，则从中提炼出一个不等式组为________．
)2>ab B．ac>bc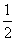
，且α＝a＋
，β＝b＋
，则α＋β的最小值为( )
其中a>1，若目标函数z＝x＋y的最大值为4，则a的值为________．