题目内容
已知椭圆| y2 |
| 5 |
| x2 |
| 4 |
| MP |
| MN |
| PN |
| MN |
(1)求动点P的轨迹C的方程;
(2)过点N作直线l与点P的轨迹C交于点A、B,分别以A、B为切点作曲线C的切线,其交点为Q,求
| NQ |
| AB |
分析:(1)由题设
+
=1,知c=1,由此能导出动点P的轨迹C的方程.
(2)由y=
x2,y′=
,知以A( x1,
)、B( x2,
)为切点的切线方程分别是 y=
x-
与y=
x-
,解得Q(
,
),设直线l的方程为y=kx+1,代入x2=4y得x2-4kx-4=0,再由根的判别式进行求解.
| y2 |
| 5 |
| x2 |
| 4 |
(2)由y=
| 1 |
| 4 |
| x |
| 2 |
| x12 |
| 4 |
| x22 |
| 4 |
| x1 |
| 2 |
| x12 |
| 4 |
| x2 |
| 2 |
| x22 |
| 4 |
| x1+x2 |
| 2 |
| x1x2 |
| 4 |
解答:解:(1)由题设知
+
=1,∴c=1,
解得N(0,1),M(0,-1),设P(x,y),
则
=(x,y+1),
=(0,2),
=(-x,1-y),
∴2y+2=2
,
∴x2=4y;
(2)y=
x2,y′=
,则以A( x1,
)、B( x2,
)为切点的切线方程分别是:
y=
x-
与y=
x-
,解得Q(
,
),设直线l的方程为y=kx+1,
(直线l与x2=2y有两个交点知k肯定存在),代入x2=4y得x2-4kx-4=0,
x1x2=-4,∴Q(
,-1),
∴
•
=(
,-2)•(x2-x1,y2-y1)
=
-2(
-
)=0.
| y2 |
| 5 |
| x2 |
| 4 |
解得N(0,1),M(0,-1),设P(x,y),
则
| MP |
| MN |
| PN |
∴2y+2=2
| (1-y)2+x2 |
∴x2=4y;
(2)y=
| 1 |
| 4 |
| x |
| 2 |
| x12 |
| 4 |
| x22 |
| 4 |
y=
| x1 |
| 2 |
| x12 |
| 4 |
| x2 |
| 2 |
| x22 |
| 4 |
| x1+x2 |
| 2 |
| x1x2 |
| 4 |
(直线l与x2=2y有两个交点知k肯定存在),代入x2=4y得x2-4kx-4=0,
x1x2=-4,∴Q(
| x1+x2 |
| 2 |
∴
| NQ |
| AB |
| x1+x2 |
| 2 |
=
| x22-x12 |
| 2 |
| x22 |
| 4 |
| x12 |
| 4 |
点评:本题考查动点P的轨迹C的方程和求
•
的值.解题时要认真审题,仔细解答,注意合理地进行等价转化.
| NQ |
| AB |

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
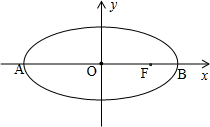 在平面直角坐标系xoy中,如图,已知椭圆
在平面直角坐标系xoy中,如图,已知椭圆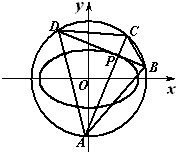 已知椭圆
已知椭圆