题目内容
函数y=
sinxcosx-sin2x的最小正周期为______,最大值为______.
| 3 |
函数y=
sinxcosx-sin2x
=
sin2x-
=
sin2x+
cos2x-
=sin(2x+
)-
,
∵ω=2,∴T=
=π;
又-1≤sin(2x+
)≤1,即sin(2x+
)的最大值为1,
∴函数的最大值为1-
=
.
故答案为:π;
| 3 |
=
| ||
| 2 |
| 1-cos2x |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=sin(2x+
| π |
| 6 |
| 1 |
| 2 |
∵ω=2,∴T=
| 2π |
| 2 |
又-1≤sin(2x+
| π |
| 6 |
| π |
| 6 |
∴函数的最大值为1-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:π;
| 1 |
| 2 |

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
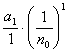 +
+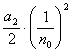 +
+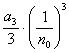 +…+
+…+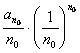
 的周期为
的周期为 


