题目内容

20．复数z=（1-i）2+$\frac{2}{1+i}$（i为虚数单位）在复平面内对应的点在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

分析 利用复数的运算法则、几何意义即可得出．

解答 解：复数z=（1-i）2+$\frac{2}{1+i}$=-2i+$\frac{2（1-i）}{（1+i）（1-i）}$=-2i+1-i=1-3i在复平面内对应的点（1，-3）在第四象限．
故选：D．

点评 本题考查了复数的运算法则、几何意义，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
13．设ϕ（x）是定义在[m，n]上的函数，若存在r∈（m，n），使得ϕ（x）在[m，r]上单调递增，在[r，n]上单调递减，则称ϕ（x）为[m，n]上的F函数．
（1）已知$ϕ（x）=\frac{x+a}{e^x}$为[1，2]上的F函数，求a的取值范围；
（2）设$ϕ（x）=px-（\frac{x^2}{2}+\frac{x^3}{3}+\frac{x^4}{4}+\frac{{p{x^5}}}{5}）$，其中p＞0，判断ϕ（x）是否为[0，p]上的F函数？
（3）已知ϕ（x）=（x2-x）（x2-x+t）为[m，n]上的F函数，求t的取值范围．
13．已知f（x）是定义在区间（0，+∞）内的单调函数，且对?x∈（0，∞），都有f[f（x）-lnx]=e+1，设f′（x）为f（x）的导函数，则函数g（x）=f（x）-f′（x）的零点个数为（　　）
A．0B．lC．2D．3
8．等差数列{an}的前n项和为Sn，且满足a4+a10=20，则S13=（　　）
A．6B．130C．200D．260
15．直线l：kx+y+4=0（k∈R）是圆C：x2+y2+4x-4y+6=0的一条对称轴，过点A（0，k）作斜率为1的直线m，则直线m被圆C所截得的弦长为（　　）
A．$\frac{\sqrt{2}}{2}$B．$\sqrt{2}$C．$\sqrt{6}$D．2$\sqrt{6}$
5．如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图，则判断框内应填入的条件是（　　）
A．i≤1009B．i＞1009C．i≤1010D．i＞1010
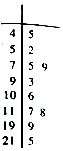12．空气质量指数（Air Quality Index，简称AQI）是定量描述空气质量状况的无量纲指数，参与空气质量评价的主要污染物为SO2、NO2、PM10、PM2.5、O3、CO等六项．空气质量按照AQI大小分为六级：一级0～50为优；二级51～100为良好；三级101～150为轻度污染；四级151～200为中度污染；五级201～300为重度污染；六级＞300为严重污染．
某人根据环境监测总站公布的数据记录了某地某月连续10天AQI的茎叶图如图所示：
（Ⅰ）利用该样本估计该地本月空气质量优良（AQI≤100）的天数；（按这个月总共30天计算）
（Ⅱ）若从样本中的空气质量不佳（AQI＞100）的这些天中，随机地抽取三天深入分析各种污染指标，求这三天的空气质量等级互不相同的概率．
8．已知函数$g（x）=（{x^2}-cosx）sin\frac{π}{6}$，对于$[{-\frac{π}{2}，\frac{π}{2}}]$上的任意x1，x2，有如下条件：
①${x_1}^3＞{x_2}^3$；②|x1|＞x2；③x1＞|x2|；④$x_1^2＞x_2^2$．
其中能使g（x1）＞g（x2）恒成立的条件序号是③④．
9．黔东南州雷山西江千户苗寨，是目前中国乃至全世界最大的苗族聚居村寨，每年来自世界各地的游客络绎不绝．假设每天到西江苗寨的游客人数ξ是服从正态分布N（2000，10000）的随机变量．则每天到西江苗寨的游客人数超过2100的概率为0.1587．（参考数据：若ξ服从N（μ，δ2），有P（μ-δ＜ξ≤μ+δ）=0.6826，P（μ-2δ＜ξ≤μ+2δ）=0.9544，P（μ-3δ＜ξ≤μ+3δ）=0.9974）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网