题目内容
20．已知x，y满足不等式$\left\{\begin{array}{l}4x-y+2≥0\\ 2x+y-8≥0\\ x≤2\end{array}\right.$，设z=$\frac{y}{x}$，则z的最大值与最小值的差为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 画出约束条件的可行域，利用目标函数的几何意义求解即可．
解答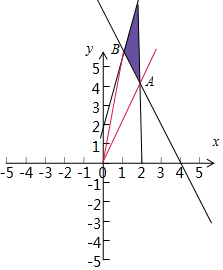 
解：x，y满足不等式$\left\{\begin{array}{l}4x-y+2≥0\\ 2x+y-8≥0\\ x≤2\end{array}\right.$，表示的可行域如图：
z=$\frac{y}{x}$的几何意义是可行域的点与终边原点连线的斜率，
由$\left\{\begin{array}{l}{x=2}\\{2x+y-8=0}\end{array}\right.$解得A（2，4），
由$\left\{\begin{array}{l}{4x-y+2=0}\\{2x+y-8=0}\end{array}\right.$解得B（1，6），
可知kOA是最小值，kOB是最大值，
则z的最大值：$\frac{6}{1}$=6，z的最小值为：$\frac{4}{2}$=2，
则z的最大值与最小值的差为：4．
故选：D．
点评 本题考查线性规划的简单应用，目标函数的几何意义是解题的关键，考查数形结合以及计算能力．
练习册系列答案
全能测控一本好卷系列答案
相关题目
10．已知对任意实数x，有f（-x）=-f（x），g（-x）=g（x），且x＜0时，导函数分别满足f′（x）＞0，g′（x）＜0，则x＞0时，成立的是（ ）
| A． | f′（x）＞0，g′（x）＜0 | B． | f′（x）＞0，g′（x）＞0 | C． | f′（x）＜0，g′（x）＜0 | D． | f′（x）＜0，g′（x）＞0 |
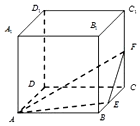如图，在棱长为1的正方体ABCD-A1B1C1D1中，点E，F分别是棱BC，CC1的中点，P是侧面BCC1B1内一点，若A1P∥平面AEF，则线段AP长度的取值范围是[$\frac{3\sqrt{2}}{4}$，$\frac{\sqrt{5}}{2}$]．