题目内容
8．把4个不同的黑球，4个不同的红球排成一排，要求黑球、红球分别在一起，不同的排法种数为1152．分析 利用捆绑法即可求出．
解答 解：分别把4个不同的黑球，4个不同的红球捆绑在一起，各看做一个复合元素，这两个复合元素全排，故有A44A44A22=1152，
故答案为：1152．
点评 本题主要考查排列组合、两个基本原理的实际应用，相邻问题用捆绑法，属于中档题．
练习册系列答案
相关题目
18．已知集合A={x|-1＜x＜3}，B={x|y=$\sqrt{1-x}$}，则A∩B=（ ）
| A． | {x|1≤x＜3} | B． | {x|x＜1} | C． | {x|-1＜x≤1} | D． | {x|-1＜x＜1} |
3．定义在R上的偶函数f（x）满足f（x）=f（x+2），当x∈[3，4]时，f（x）=x-2，则（ ）
| A． | f（sin$\frac{1}{2}$）＜f（cos$\frac{1}{2}$） | B． | f（sin$\frac{π}{3}$）＞f（cos$\frac{π}{3}$） | C． | f（sin1）＜f（cos1） | D． | f（sin$\frac{π}{2}$）＞f（cos$\frac{π}{2}$） |
13．（$\overrightarrow{AB}$+$\overrightarrow{MB}$）+（$\overrightarrow{BO}$+$\overrightarrow{OM}$）+$\overrightarrow{BA}$化简后为（ ）
| A． | $\overrightarrow{0}$ | B． | $\overrightarrow{AB}$ | C． | $\overrightarrow{BA}$ | D． | $\overrightarrow{OM}$ |
3．
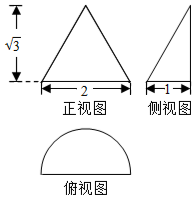已知某几何体的三视图如图所示，则该几何体的表面积为（ ）
已知某几何体的三视图如图所示，则该几何体的表面积为（ ）| A． | $\frac{5π}{2}+\sqrt{3}$ | B． | $\frac{3π}{2}+2$ | C． | $\frac{π}{2}+\sqrt{3}$ | D． | $\frac{3π}{2}+\sqrt{3}$ |