题目内容
已知函数f(x)=x•lnx,g(x)=
.
(Ⅰ)求函数f(x)的极值和单调区间:
(Ⅱ)对于x>0的任意实数,不等式g(x)≤ax-1≤f(x)恒成立,求实数a的取值;
(Ⅲ)数列{1nn}(n∈N*)的前n项和为Sn,求证:
≤Sn≤
.
| lnx |
| x |
(Ⅰ)求函数f(x)的极值和单调区间:
(Ⅱ)对于x>0的任意实数,不等式g(x)≤ax-1≤f(x)恒成立,求实数a的取值;
(Ⅲ)数列{1nn}(n∈N*)的前n项和为Sn,求证:
| (n-1)2 |
| 2n |
| n(n-1)(n+1) |
| 3 |
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(Ⅰ)求导数,利用导数的正负,确定函数的单调区间,从而可得函数f(x)的极值;
(Ⅱ)分离参数,求最值,即可求实数a的取值;
(Ⅲ)利用数学归纳法进行证明即可.
(Ⅱ)分离参数,求最值,即可求实数a的取值;
(Ⅲ)利用数学归纳法进行证明即可.
解答:
(Ⅰ)解:∵f(x)=x•lnx,
∴f′(x)=1+lnx,
令f′(x)>0,可得x>
,f′(x)<0,可得0<x<
,
∴函数的单调递增区间为(
,+∞),单调减区间为(0,
),
∴x=
时,函数取得极小值-
;
(Ⅱ)解:∵对于x>0的任意实数,不等式g(x)≤ax-1≤f(x)恒成立,
∴
≤a≤lnx+
.
设m(x)=
,n(x)=lnx+
,则
m′(x)=
(x>0),令h(x)=1-x-2lnx,则h′(x)=-1-
<0,
∴h(x)在(0,+∞)上单调递增且h(1)=0,
∴x∈(0,1)时,m′(x)>0,x∈(1,+∞)时,m′(x)<0,
∴m(x)在(0,1)是单调递增,在(1,+∞)上单调递减,
∴m(x)的最大值为1,
∴a≥1.
同理n(x)在(0,1)是单调递减,在(1,+∞)上单调递增,
∴n(x)的最小值为1,
∴a≤1,
∴a=1;
(Ⅲ)证明:①n=1是,S1=0,不等式成立;
②假设n=k时,结论成立,即
≤Sk≤
.
由(Ⅱ),用k+1代替(Ⅱ)中的x,可得
≤k≤(k+1)ln(k+1),
∴
≤ln(k+1)≤k(k+1),
∴Sk+1=Sk+ln(k+1)≤
+k(k+1)=
,
Sk+1=Sk+ln(k+1)≥
+
≥
,即n=k+1时,结论成立.
由①②可知
≤Sn≤
.
∴f′(x)=1+lnx,
令f′(x)>0,可得x>
| 1 |
| e |
| 1 |
| e |
∴函数的单调递增区间为(
| 1 |
| e |
| 1 |
| e |
∴x=
| 1 |
| e |
| 1 |
| e |
(Ⅱ)解:∵对于x>0的任意实数,不等式g(x)≤ax-1≤f(x)恒成立,
∴
| lnx+x |
| x2 |
| 1 |
| x |
设m(x)=
| lnx+x |
| x2 |
| 1 |
| x |
m′(x)=
| 1-x-2lnx |
| x3 |
| 1 |
| x |
∴h(x)在(0,+∞)上单调递增且h(1)=0,
∴x∈(0,1)时,m′(x)>0,x∈(1,+∞)时,m′(x)<0,
∴m(x)在(0,1)是单调递增,在(1,+∞)上单调递减,
∴m(x)的最大值为1,
∴a≥1.
同理n(x)在(0,1)是单调递减,在(1,+∞)上单调递增,
∴n(x)的最小值为1,
∴a≤1,
∴a=1;
(Ⅲ)证明:①n=1是,S1=0,不等式成立;
②假设n=k时,结论成立,即
| (k-1)2 |
| 2k |
| k(k-1)(k+1) |
| 3 |
由(Ⅱ),用k+1代替(Ⅱ)中的x,可得
| ln(k+1) |
| k+1 |
∴
| k |
| k+1 |
∴Sk+1=Sk+ln(k+1)≤
| k(k-1)(k+1) |
| 3 |
| k(k+1)(k+2) |
| 3 |
Sk+1=Sk+ln(k+1)≥
| (k-1)2 |
| 2k |
| k |
| k+1 |
| k2 |
| 2k(k+1) |
由①②可知
| (n-1)2 |
| 2n |
| n(n-1)(n+1) |
| 3 |
点评:本题考查导数知识的综合运用,考查函数的单调性与极值,考查不等式的证明,考查数学归纳法,考查学生分析解决问题的能力,有难度.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
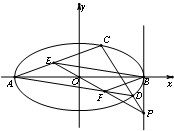 如图,在平面直角坐标系xOy中,A、B分别是椭圆:
如图,在平面直角坐标系xOy中,A、B分别是椭圆: