题目内容
已知p: ≤2,q:x2-2x+1-m2≤0
≤2,q:x2-2x+1-m2≤0 ,若綈p 是綈q的必要不充分条件,求实数m的取值范围.
,若綈p 是綈q的必要不充分条件,求实数m的取值范围.
解析:由题意知,命题:由綈p是綈q的必要不充分条件的等价命题即逆否命题为:p是q的充分不必要条件.
p: ≤2⇒-2≤
≤2⇒-2≤ -1≤2⇒-2≤x≤10.
-1≤2⇒-2≤x≤10.
q:x2-2x+1-m2≤0⇒[x-(1-m)][x-(1+m)]≤0(*)
∵p是q的充分不必要条件,
∴不等式 ≤2的解集是x2-2x+1-m2≤0(m>0)的真子集.
≤2的解集是x2-2x+1-m2≤0(m>0)的真子集.
又∵m>0,∴不等式(*)的解集为{x|1-m≤x≤1+m}.
又∵1-m=-2与1+m=10不同时成立,
∴ ⇒
⇒ ∴m≥9.
∴m≥9.
∴实数m的取值范围是[9,+∞).

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
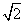 的直线与曲线E相切,求此时直线到原点的距离.
的直线与曲线E相切,求此时直线到原点的距离.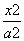 +
+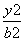 =1(a>b>0)过点P(3,1),其左、右焦点分别为F1,F2,且
=1(a>b>0)过点P(3,1),其左、右焦点分别为F1,F2,且 ·
·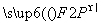 =-6.
=-6. 命题“∃x∈R,使得x2+(1-a)x+1<0”是真命题,则实数a的取值范围是______________.
命题“∃x∈R,使得x2+(1-a)x+1<0”是真命题,则实数a的取值范围是______________. ”的( )
”的( ) B.
B. C.-
C.- D.-
D.- 三点共线,则m的值
三点共线,则m的值 为________.
为________.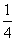 B.
B. C.
C. D.
D.
 函数f(x)=(cos 2xcos x+sin 2xsin x)sin x,x∈R,则f(x)是( )
函数f(x)=(cos 2xcos x+sin 2xsin x)sin x,x∈R,则f(x)是( ) 的奇函数
的奇函数