题目内容
设f(x)=|x-3|+|x-4|
(Ⅰ)求函数g(x)=
的定义域;
(Ⅱ)若存在实数x满足f(x)≤ax-1,试求实数a的取值范围.
(Ⅰ)求函数g(x)=
| 2-f(x) |
(Ⅱ)若存在实数x满足f(x)≤ax-1,试求实数a的取值范围.
考点:函数的图象
专题:函数的性质及应用
分析:(Ⅰ)根据函数成立的条件,即可求函数g(x)=
的定义域;
(Ⅱ)作出f(x)的图象,利用数形结合即可得到结论.
| 2-f(x) |
(Ⅱ)作出f(x)的图象,利用数形结合即可得到结论.
解答:
 解:(Ⅰ)f(x)=|x-3|+|x-4|=
解:(Ⅰ)f(x)=|x-3|+|x-4|=
,
要使函数g(x)有意义,则2-f(x)≥0,
即f(x)≤2,
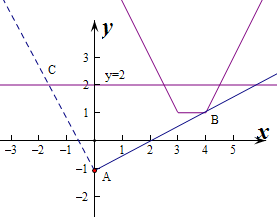
作函数y=f(x)的图象,它与直线y=2交点的横坐标为
和
,
由图象知f(x)≤2的解为
≤x≤
,
即函数的定义域为[
,
].
(Ⅱ)函数y=ax-1的图象是过点(0,-1)的直线.
当且仅当函数y=f(x)与直线y=ax-1有公共点时,存在题设的x.
由图象知,当x=4时,y=1,即B(4,1),当直线y=ax-1经过点B时,满足条件,
此时1=4a-1,解得a=
,
当a≥
时,满足条件.
当直线y=ax-1与y=7-2x平行时,不满足条件,此时a=-2,
即当a<0时,要满足条件,则a<-2,
综上a取值范围为(-∞,-2)∪[
,+∞].
 解:(Ⅰ)f(x)=|x-3|+|x-4|=
解:(Ⅰ)f(x)=|x-3|+|x-4|=
|
要使函数g(x)有意义,则2-f(x)≥0,
即f(x)≤2,
作函数y=f(x)的图象,它与直线y=2交点的横坐标为
| 5 |
| 2 |
| 9 |
| 2 |
由图象知f(x)≤2的解为
| 5 |
| 2 |
| 9 |
| 2 |
即函数的定义域为[
| 5 |
| 2 |
| 9 |
| 2 |
(Ⅱ)函数y=ax-1的图象是过点(0,-1)的直线.
当且仅当函数y=f(x)与直线y=ax-1有公共点时,存在题设的x.
由图象知,当x=4时,y=1,即B(4,1),当直线y=ax-1经过点B时,满足条件,
此时1=4a-1,解得a=
| 1 |
| 2 |
当a≥
| 1 |
| 2 |
当直线y=ax-1与y=7-2x平行时,不满足条件,此时a=-2,
即当a<0时,要满足条件,则a<-2,
综上a取值范围为(-∞,-2)∪[
| 1 |
| 2 |
点评:本题主要考查绝对值函数的图象和性质,利用数形结合是解决本题的关键.考查学生的作图能力.

练习册系列答案
相关题目
 如图,E是以AB为直径的半圆上异于A、B的点,矩形ABCD所在的平面垂直于该半圆所在的平面,且AB=2AD=2.
如图,E是以AB为直径的半圆上异于A、B的点,矩形ABCD所在的平面垂直于该半圆所在的平面,且AB=2AD=2. 已知三棱柱ABC-A1B1C1中,平面A1AC⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2.
已知三棱柱ABC-A1B1C1中,平面A1AC⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2.