Question

记集合A={（x，y）|x²+y²≤16}和集合B={（x，y）|x+y+4≥0，x≤0，y≤0}表示的平面区域分别为Ω₁，Ω₂，若Ω₁在区域内任取一点M（x，y），则M落在区域Ω₂内的概率为（　　）

• A、

  1

  2π

• B、

  1

  π

• C、

  1

  4

• D、

  π-2

  4π

Answer 1

考点：几何概型

专题：概率与统计

分析：根据题意可知，是与面积有关的几何概率，要求M落在区域Ω₂内的概率，只要求A、B所表示区域的面积，然后代入概率公式P=

区域Ω2的面积

区域Ω1的面积

，计算即可得答案．

解答： 解：根据题意可得集合A={（x，y）|x²+y²≤16}所表示的区域即为如图所表示的圆及内部的平面区域，面积为16π，
集合B={（x，y）|x+y+4≥0，x≤0，y≤0}表示的平面区域即为图中的Rt△AOB，

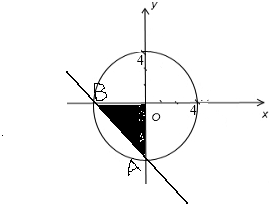
S_△AOB=

1

2

×4×4=8，
根据几何概率的计算公式可得P=

8

16π

=

1

2π

；
故选：A．

点评：本题主要考查了几何概率的计算，本题是与面积有关的几何概率模型．解决本题的关键是要准确求出两区域的面积．