题目内容
已知函数 (
( )在
)在 取到极值,
取到极值,
(I)写出函数 的解析式;
的解析式;
(II)若 ,求
,求 的值;
的值;
(Ⅲ)从区间 上的任取一个
上的任取一个 ,若
,若 在点
在点 处的切线的斜率为
处的切线的斜率为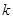 ,求
,求 的概率.
的概率.
(I)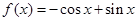 ;(II)3;(Ⅲ)
;(II)3;(Ⅲ)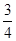 ;
;
解析试题分析:(1)由已知可得: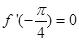 ,
,
即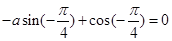 ,得
,得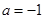
故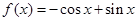
(2)由 ,得
,得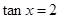
又由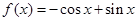 ,得
,得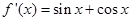
故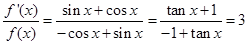
(3)由 在
在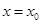 处的切线斜率
处的切线斜率 ,可得
,可得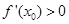 ,即
,即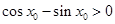
得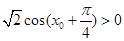
又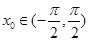 ,可得
,可得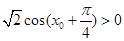 时,
时,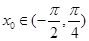 故
故 的概率为
的概率为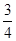
考点:利用导数研究函数的极值;三角函数的化简与求值;导数的几何意义。
点评:?关于sinx、cosx的三角齐次式的命题多次出现在近年的试题中?通过对这类题型的研究?我们不难发现此类题型的一般解题规律:直接或间接地已知tanx的值,要求关于sinx、cosx的某些三角齐次式的值。解决的主要方法是:分子、分母同除以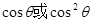 ,变成关于
,变成关于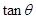 的式子。
的式子。

练习册系列答案
相关题目

 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 内角A,B,C的对边分别为
内角A,B,C的对边分别为 ,若向量
,若向量 共线,求
共线,求 的值。
的值。 ,
, ,且
,且 .
.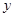 表示成
表示成 的函数
的函数 ,并求
,并求 ,
, 、
、 、
、 分别为
分别为 的三个内角
的三个内角 、
、 、
、 对应的边长,若
对应的边长,若 且
且 ,求
,求 的最大值.
的最大值. ,
, .
. 的最大值;
的最大值; 中,角
中,角 、
、 的对边分别为
的对边分别为 、
、 ,若
,若 且
且 ,
, 的大小.
的大小. ,且
,且 是方程
是方程 的两根.
的两根. 的值. (2)求
的值. (2)求 的值.
的值.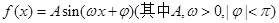 的部分图像
的部分图像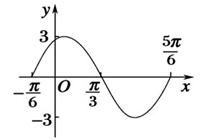
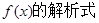
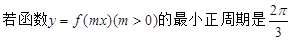 ,
,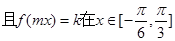 上有
上有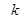 的取值范围
的取值范围 ,其中
,其中
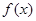 在区间
在区间 上的值域;
上的值域; 中,
中, .
. ,
, 分别是角
分别是角 的对边,
的对边,  ,且
,且
 ,求边
,求边 的一条对称轴为
的一条对称轴为 ,且
,且
 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 ,若
,若 ,且
,且 .
. 的值; (2)若
的值; (2)若 ,求△
,求△