题目内容
(本小题满分12分)已知 ,
, ,且
,且 .
.
(I)将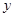 表示成
表示成 的函数
的函数 ,并求
,并求 的最小正周期;
的最小正周期;
(II)记 的最大值为
的最大值为 ,
, 、
、 、
、 分别为
分别为 的三个内角
的三个内角 、
、 、
、 对应的边长,若
对应的边长,若 且
且 ,求
,求 的最大值.
的最大值.
4.
解析试题分析:(I)由 得
得 ………………
………………
即
所以 ,………………
,……………… 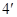
又
所以函数 的最小正周期为
的最小正周期为 …………………
…………………
(II)由(I)易得 ……………………
……………………
于是由 即
即 ,
,
因为 为三角形的内角,故
为三角形的内角,故 ……………………
……………………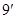
由余弦定理 得
得 …………
…………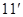
解得
于是当且仅当 时,
时, 的最大值为
的最大值为 .………………………
.……………………… 
考点:向量平行的条件;三角函数的周期公式;余弦定理。
点评:三角函数和其他知识点相结合往往是第一道大题,一般较为简单,应该是必得分的题目。而有些同学在学习中认为这类题简单,自己一定会,从而忽略了对它的练习,因此导致考试时不能得满分,甚至不能得分。因此我们在平常训练的时候就要要求自己“会而对,对而全”。

练习册系列答案
相关题目
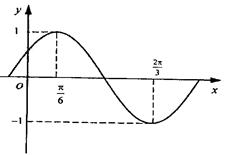
 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为 .
. 的值;
的值; 求
求 的取值范围。
的取值范围。 ,函数
,函数 (其中
(其中 的图像在
的图像在 轴右侧的第一个最高点(即函数取得最大值的点)为
轴右侧的第一个最高点(即函数取得最大值的点)为
 ,在原点右侧与
,在原点右侧与 轴的第一个交点为
轴的第一个交点为
 .
. 的表达式;
的表达式; 上是否存在对称轴,存在求出方程;否则说明理由;
上是否存在对称轴,存在求出方程;否则说明理由;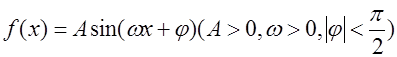
 的最小正周期及解析式;
的最小正周期及解析式; ,求函数
,求函数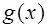 在区间 R上的最大值和最小值及对应的x的集合.
在区间 R上的最大值和最小值及对应的x的集合.

 ,
, 的最小值是
的最小值是 ,最大值是
,最大值是 ,求实数
,求实数 的值.
的值.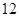 分)
分) .
. 的最大值及相应的
的最大值及相应的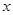 的值.
的值. .
. 的最大值及最小正周期;
的最大值及最小正周期; 满足
满足 ,求
,求 (
( )在
)在 取到极值,
取到极值, 的解析式;
的解析式; ,求
,求 的值;
的值; 上的任取一个
上的任取一个 ,若
,若 处的切线的斜率为
处的切线的斜率为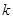 ,求
,求 的概率.
的概率. ,
, ,求该函数的单调递增区间。
,求该函数的单调递增区间。