题目内容
(本小题满分12分)
已知函数 ,
, .
.
(1)求 的最大值;
的最大值;
(2)设△ 中,角
中,角 、
、 的对边分别为
的对边分别为 、
、 ,若
,若 且
且 ,
,
求角 的大小.
的大小.
(1) ;(2)
;(2) 。
。
解析试题分析:(1)
 ………2分
………2分
 .(注:也可以化为
.(注:也可以化为 ) …4分
) …4分
 的最大值为
的最大值为 . ………………………………6分
. ………………………………6分
(2)因为 ,由(1)和正弦定理,得
,由(1)和正弦定理,得 .…………7分
.…………7分
又 ,所以
,所以 ,即
,即 , ………………8分
, ………………8分
而 是三角形的内角,所以
是三角形的内角,所以 ,故
,故 ,
, ,…………10分
,…………10分
又 ,所以
,所以 ,
, ,
, . ……… ……12分
. ……… ……12分
考点:和差公式;三角函数最值的求法;正弦定理;同角三角函数关系式;三角形内的隐含条件。
点评:对于式子“ ”容易出错,本题已给出A为三角形的内角,所以这里可以约掉sinA.若没有告诉角A的范围,就不能约掉sinA了。其解决问题的方法应该是:由
”容易出错,本题已给出A为三角形的内角,所以这里可以约掉sinA.若没有告诉角A的范围,就不能约掉sinA了。其解决问题的方法应该是:由 得
得
 。
。

练习册系列答案
相关题目
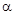 的扇形,制成一个圆锥形的漏斗,问圆心角
的扇形,制成一个圆锥形的漏斗,问圆心角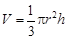 ,其中圆锥的底面半径为r,高为h)
,其中圆锥的底面半径为r,高为h)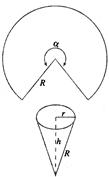
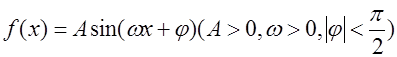
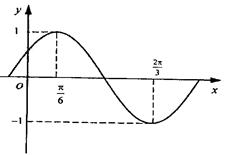
 的最小正周期及解析式;
的最小正周期及解析式; ,求函数
,求函数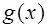 在区间 R上的最大值和最小值及对应的x的集合.
在区间 R上的最大值和最小值及对应的x的集合.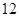 分)
分) .
. 的最大值及相应的
的最大值及相应的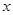 的值.
的值. .
. 的最大值及最小正周期;
的最大值及最小正周期; 满足
满足 ,求
,求 ,
, 其中
其中 ,记函数
,记函数 ,若函数
,若函数 的图像与直线
的图像与直线 (
( 为常数)相切,并且切点的横坐标依次成公差为
为常数)相切,并且切点的横坐标依次成公差为 的等差数列。
的等差数列。 的图像向左平移
的图像向左平移 ,得到
,得到 的图像,当
的图像,当 时,
时, 的交点横坐标成等比数列,求钝角
的交点横坐标成等比数列,求钝角 的值。
的值。 (
( )在
)在 取到极值,
取到极值, 的解析式;
的解析式; ,求
,求 的值;
的值; 上的任取一个
上的任取一个 ,若
,若 处的切线的斜率为
处的切线的斜率为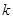 ,求
,求 的概率.
的概率. ,求
,求 的值.
的值. (
( )的最小正周期为
)的最小正周期为 ,
,  时,求函数
时,求函数 的最小值;
的最小值; ,若
,若 ,且
,且 ,求
,求 的值。
的值。