题目内容
(本小题满分14分)
已知函数
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)已知 内角A,B,C的对边分别为
内角A,B,C的对边分别为 ,若向量
,若向量 共线,求
共线,求 的值。
的值。
(1)最小正周期T=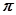 ,递增区间为
,递增区间为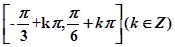
(2)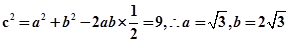 。
。
解析试题分析:(1)f(x)=2sin(2x+ )+1
)+1
最小正周期T=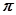 ,递增区间为
,递增区间为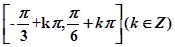 (7分)
(7分)
(2)f(C)=2sin(2C+ )+1="2,"
)+1="2," 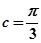 ,因为向量
,因为向量 共线,
共线,
所以sinB=2sinA,,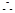 b=2a,由余弦定理可得
b=2a,由余弦定理可得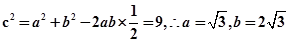 (14分)
(14分)
考点:本题主要考查平面向量共线的条件,三角恒等变换,三角函数的周期、单调、最值等性质,余弦定理;考查三角函数与平面向量的综合运用能力和化归与转化思想。
点评:典型题,为研究三角函数的图象和性质,往往需要将函数“化一”,这是常考题型。本题首先通过平面向量的坐标运算,计算向量的数量积得到函数F(x)的表达式,并运用“三角公式”进行化简,为进一步解题奠定了基础。

练习册系列答案
相关题目

 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为 .
. 的值;
的值; 求
求 的取值范围。
的取值范围。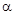 的扇形,制成一个圆锥形的漏斗,问圆心角
的扇形,制成一个圆锥形的漏斗,问圆心角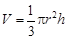 ,其中圆锥的底面半径为r,高为h)
,其中圆锥的底面半径为r,高为h)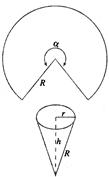
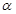 是第二象限角,且
是第二象限角,且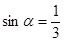 求
求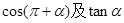 的值;
的值; ,若
,若 对一切
对一切 恒成立.求实数
恒成立.求实数 的取值范围.
的取值范围.  ,函数
,函数 (其中
(其中 的图像在
的图像在 轴右侧的第一个最高点(即函数取得最大值的点)为
轴右侧的第一个最高点(即函数取得最大值的点)为
 ,在原点右侧与
,在原点右侧与 轴的第一个交点为
轴的第一个交点为
 .
. 的表达式;
的表达式; 上是否存在对称轴,存在求出方程;否则说明理由;
上是否存在对称轴,存在求出方程;否则说明理由;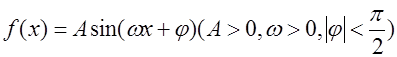
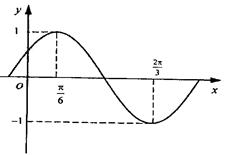
 的最小正周期及解析式;
的最小正周期及解析式; ,求函数
,求函数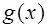 在区间 R上的最大值和最小值及对应的x的集合.
在区间 R上的最大值和最小值及对应的x的集合. (
( )在
)在 取到极值,
取到极值, 的解析式;
的解析式; ,求
,求 的值;
的值; 上的任取一个
上的任取一个 ,若
,若 处的切线的斜率为
处的切线的斜率为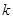 ,求
,求 的概率.
的概率.