题目内容
 如图,B,C为圆O上的两个点,P为CB延长线上一点,PA为圆O的切线,A为切点.若PA=2,BC=3,则PB=
如图,B,C为圆O上的两个点,P为CB延长线上一点,PA为圆O的切线,A为切点.若PA=2,BC=3,则PB=| AC | AB |
分析:根据PA切圆O于点A,利用切割线定理得PA2=PB•PC,代入数据得到关于PB的方程,解之可得PB=1.再由弦切角定理证出∠BAP=∠C,结合∠APB=∠CPA得到△CPA∽△APB,即可算出
的值.
| AC |
| AB |
解答:解:∵PA是圆O的切线,PBC是割线,∴PA2=PB•PC,
∵PA=2、BC=3,
∴22=PB•(PB+3),解得PB=1(舍负).
∵PA切圆O于点A,∴∠BAP=∠C,
又∵∠APB=∠CPA,
∴△CPA∽△APB,可得
=
=2.
故答案为:1,2
∵PA=2、BC=3,
∴22=PB•(PB+3),解得PB=1(舍负).
∵PA切圆O于点A,∴∠BAP=∠C,
又∵∠APB=∠CPA,
∴△CPA∽△APB,可得
| AC |
| AB |
| PA |
| PB |
故答案为:1,2
点评:本题给出圆O的切线与割线,求PB的长并求两条线段的比值.着重考查了弦切角定理、切割线定理、相似三角形的判定与性质等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
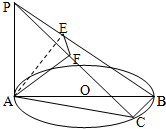 如图,AB为圆O的直径,点C为圆O上异于A、B的一点,PA⊥平面ABC,点A在PB、PC上的射影分别为点E、F.
如图,AB为圆O的直径,点C为圆O上异于A、B的一点,PA⊥平面ABC,点A在PB、PC上的射影分别为点E、F. 如图,AB为圆O的直径,C为圆O上一点,AP和过C的切线互相垂直,垂足为P,过B的切线交过C的切线于T,PB交圆O于Q,若∠BTC=120°,AB=4,则PQ•PB=
如图,AB为圆O的直径,C为圆O上一点,AP和过C的切线互相垂直,垂足为P,过B的切线交过C的切线于T,PB交圆O于Q,若∠BTC=120°,AB=4,则PQ•PB= (2012•衡阳模拟)如图所示,已知圆O直径AB=
(2012•衡阳模拟)如图所示,已知圆O直径AB= 如图所示,已知A,B,C是圆O上三个点,AB弧等于BC弧,D为弧AC上一点,过点A做圆O的切线交BD延长线于E
如图所示,已知A,B,C是圆O上三个点,AB弧等于BC弧,D为弧AC上一点,过点A做圆O的切线交BD延长线于E