题目内容
在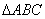 中,三内角
中,三内角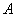 ,
,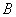 ,
,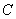 的对边分别为
的对边分别为 ,
,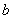 ,
, 且
且 ,
, ,
, 为
为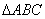 的面积,则
的面积,则 的最大值为 .
的最大值为 .
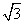 . ∵
. ∵ ,∴
,∴ ,∴
,∴ ,
,
设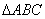 外接圆的半径为
外接圆的半径为 ,则
,则 ,∴
,∴ ,
,
∴
 ,故
,故 的最大值为
的最大值为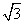 .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
题目内容
在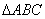 中,三内角
中,三内角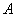 ,
,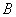 ,
,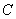 的对边分别为
的对边分别为 ,
,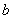 ,
, 且
且 ,
, ,
, 为
为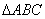 的面积,则
的面积,则 的最大值为 .
的最大值为 .
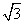 . ∵
. ∵ ,∴
,∴ ,∴
,∴ ,
,
设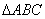 外接圆的半径为
外接圆的半径为 ,则
,则 ,∴
,∴ ,
,
∴
 ,故
,故 的最大值为
的最大值为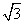 .
.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案