题目内容
19．不等式$\sqrt{x-1}$＜3的解集是[1，8）．分析 由$\sqrt{x-1}$＜3得$\left\{\begin{array}{l}{x-1≥0}\\{x-1＜9}\end{array}\right.$，解得即可．
解答 解：由$\sqrt{x-1}$＜3得$\left\{\begin{array}{l}{x-1≥0}\\{x-1＜9}\end{array}\right.$，解得1≤x＜8，
故不等式的解集为[1，8），
故答案为：[1，8）
点评 本题考查了不等式的解法，属于基础题．
练习册系列答案
相关题目
9．
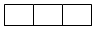用2种不同颜色给图中3个矩形随机涂色，每个矩形只涂一种颜色，则3个矩形中相邻矩形颜色不同的概率是（ ）
用2种不同颜色给图中3个矩形随机涂色，每个矩形只涂一种颜色，则3个矩形中相邻矩形颜色不同的概率是（ ）| A． | $\frac{1}{8}$ | B． | $\frac{1}{4}$ | C． | $\frac{3}{8}$ | D． | $\frac{1}{2}$ |
14．用红、黄、蓝、绿4种颜色为一个五棱锥的六个顶点着色，要求每一条棱的两个端点着不同的颜色，则不同的着色方案共有 （ ）种？
| A． | 120 | B． | 140 | C． | 180 | D． | 240 |
8．
如图，在半径为1，圆心角为90°的直角扇形OAB中，Q为AB上一点，点P在扇形内（含边界），且$\overrightarrow{OP}$=t$\overrightarrow{OA}$+（1-t）$\overrightarrow{OB}$（0≤t≤1），则$\overrightarrow{OP}$$•\overrightarrow{OQ}$的最大值为（ ）
如图，在半径为1，圆心角为90°的直角扇形OAB中，Q为AB上一点，点P在扇形内（含边界），且$\overrightarrow{OP}$=t$\overrightarrow{OA}$+（1-t）$\overrightarrow{OB}$（0≤t≤1），则$\overrightarrow{OP}$$•\overrightarrow{OQ}$的最大值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{3}{4}$ | D． | 1 |