题目内容
观察下列两个结论:
(Ⅰ)若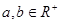 ,且
,且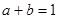 ,则
,则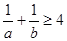 ;
;
(Ⅱ)若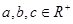 ,且
,且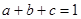 ,则
,则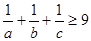 ;
;
先证明结论(Ⅱ),再类比(Ⅰ)(Ⅱ)结论,请你写出一个关于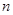 个正数
个正数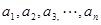 的结论?(写出结论,不必证明。
的结论?(写出结论,不必证明。
(1)运用不等式的思想,作差法比较大小是最重要的方法之一。
(2)能结合均值不等式来求证不等式的证明问题,关键是一正二定三相等,来解决。
(3)归纳猜想来得到相关的表达式,注意不等式左右两边的特点。
解析试题分析:证明:∵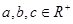 ,且
,且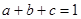
∴ 3分
3分 5分
5分 7分
7分
(当且仅当 时,等号成立) 8分(若用分析法证明也相应给分。)
时,等号成立) 8分(若用分析法证明也相应给分。)
猜测:若 ,且
,且 ,
,
则
 12分
12分
考点:不等式的证明
点评:解决的关键是利用均值不等式或者作差法来比较大小,并归纳猜想得到证明。属于中档题。

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
已知点 在如图所示的平面区域(阴影部分)内运动,则
在如图所示的平面区域(阴影部分)内运动,则 的最大值是( )
的最大值是( )
| A.1 | B.3 | C.5 | D.13 |
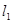 :y=-1,过定点F与直线
:y=-1,过定点F与直线 交动点C的轨迹于两点P、Q,交直线
交动点C的轨迹于两点P、Q,交直线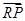 ·
· 的最小值;
的最小值;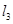 交动点C的轨迹于两点R、T,问四边形PRQT的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
交动点C的轨迹于两点R、T,问四边形PRQT的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由. 均为正数,且
均为正数,且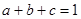
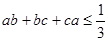 ;
;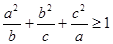 .
.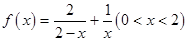 .
. 的最小值及相应
的最小值及相应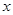 的值;
的值;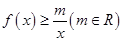 .
. ,两侧墙的长为
,两侧墙的长为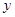 ,一套简易房所用材料费为p,试用
,一套简易房所用材料费为p,试用 。
。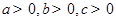 ,且
,且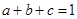 ,证明不等式:
,证明不等式: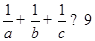
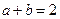 ,求证:
,求证: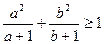
 ,设平面区域
,设平面区域 ,若圆心
,若圆心 ,且圆
,且圆 与
与 轴相切,则
轴相切,则 的最大值为 ( )
的最大值为 ( )