题目内容
直线 与椭圆
与椭圆 交于
交于 两点,以线段
两点,以线段 为直径的圆过椭圆的右焦点,则椭圆
为直径的圆过椭圆的右焦点,则椭圆 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
C
解析试题分析:直线 与椭圆
与椭圆 联立方程得
联立方程得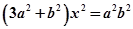 ,设
,设 右焦点为
右焦点为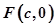
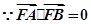 代入坐标得
代入坐标得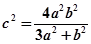 整理得
整理得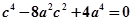
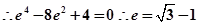
考点:直线与椭圆的位置关系及离心率
点评:求离心率需要找关于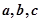 的齐次方程或不等式,求离心率时高考必考题型,本题难度较大
的齐次方程或不等式,求离心率时高考必考题型,本题难度较大

练习册系列答案
相关题目
圆 上的点到直线
上的点到直线 距离的最大值是( )
距离的最大值是( )
A. | B. | C. | D. |
直线 被圆
被圆 所截得的弦长为( )
所截得的弦长为( )
A. | B. | C. | D. |
已知圆 ,圆
,圆 ,则两圆公切线的条数有( )
,则两圆公切线的条数有( )
A. 条 条 | B. 条 条 | C. 条 条 | D. 条 条 |
若直线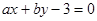 和圆
和圆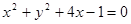 相切与点
相切与点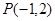 ,则
,则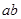 的值为( )
的值为( )
A.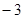 | B.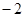 | C. | D.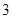 |
若直线3x+y+a=0过圆x2+y2+2x-4y=0的圆心,则a的值为( ).
| A.-1 | B.1 | C.3 | D.-3 |
已知Rt△ABC的两条直角边长分别为a、b,斜边长为c,则直线ax+by+c=0与圆x2+y2=1的位置关系是( )
| A.相交 | B.相切 | C.相离 | D.相切或相交 |
若直线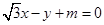 与圆
与圆 相切, 则实数m等于
相切, 则实数m等于
A. 或 或 | B. 或 或 |
C. 或 或 | D. 或 或 |
已知圆的方程为 ,则其圆心坐标和半径分别为( )
,则其圆心坐标和半径分别为( )
| A.(3, -1),r = 4 | B.(3, -1),r = 2 |
| C.(-3, 1),r = 2 | D.(-3, 1),r = 4 |