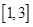题目内容
直线 被圆
被圆 所截得的弦长为( )
所截得的弦长为( )
A. | B. | C. | D. |
B
解析试题分析:∵圆心(4,0)到直线x-y-2=0的距离为 ,∴截得的弦长为
,∴截得的弦长为 ,故选B
,故选B
考点:本题考查了直线与圆的位置关系
点评:求直线与圆的弦长问题要注意利用重要的直角三角形处理。

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
若圆 的半径为1,圆心在第一象限,且与直线
的半径为1,圆心在第一象限,且与直线 和
和 轴相切,则该圆的标准方程是( )
轴相切,则该圆的标准方程是( )
A. | B. |
C. | D. |
已知两点 ,点
,点 是圆
是圆 上任意一点,则
上任意一点,则 面积的最小值是( ).
面积的最小值是( ).
A. | B. | C. | D. |
直线 被圆
被圆 截得的弦长为( )
截得的弦长为( )
A. | B. | C. | D. |
直线 与椭圆
与椭圆 交于
交于 两点,以线段
两点,以线段 为直径的圆过椭圆的右焦点,则椭圆
为直径的圆过椭圆的右焦点,则椭圆 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
直线 按向量
按向量 平移后与圆
平移后与圆 相切,则
相切,则 的值等于( )
的值等于( )
A.8或 | B.6或 | C.4或 | D.2或 |
若点 在圆C:
在圆C: 的外部,则直线
的外部,则直线 与圆C的位置关系是( )
与圆C的位置关系是( )
| A.相切 | B.相离 | C.相交 | D.相交或相切 |
 和点B(3,0),P是圆上一点,线段BP的垂直平分线交CP于M点,则M点的轨迹方程是( )。
和点B(3,0),P是圆上一点,线段BP的垂直平分线交CP于M点,则M点的轨迹方程是( )。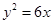 .
. 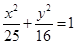


 和圆
和圆 ,圆心为M,点
,圆心为M,点 在直线
在直线 上,若圆
上,若圆 与直线
与直线 至少有一个公共点
至少有一个公共点 ,且
,且 ,则点
,则点