题目内容
若直线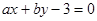 和圆
和圆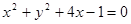 相切与点
相切与点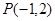 ,则
,则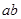 的值为( )
的值为( )
A.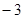 | B.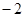 | C. | D.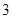 |
C
解析试题分析:因为直线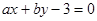 和圆
和圆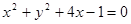 相切与点
相切与点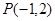 ,所以圆心C(-2,0)到切线
,所以圆心C(-2,0)到切线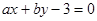 的距离等于|PC|,从而
的距离等于|PC|,从而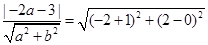 ,且
,且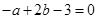 ,解得a=1,b=2,所以
,解得a=1,b=2,所以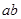 的值为2,故选C。
的值为2,故选C。
考点:本题主要考查直线与圆的位置关系。
点评:基础题,直线与圆相切,圆心到切线距离等于半径。

练习册系列答案
相关题目
直线过点P(0,2),且截圆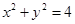 所得的弦长为2,则直线的斜率为
所得的弦长为2,则直线的斜率为
A.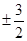 | B.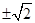 | C.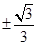 | D.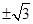 |
圆 上的点到直线
上的点到直线 的距离最大值是( )
的距离最大值是( )
| A.2 | B. | C. | D. |
直线 与椭圆
与椭圆 交于
交于 两点,以线段
两点,以线段 为直径的圆过椭圆的右焦点,则椭圆
为直径的圆过椭圆的右焦点,则椭圆 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
直线 被圆
被圆 所截得的弦长为( )
所截得的弦长为( )
A. | B. | C. | D.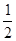 |
设A,B为直线 与圆
与圆 的两个交点,则|AB|=( )
的两个交点,则|AB|=( )
| A.1 | B. | C. | D.2 |
若点 在圆C:
在圆C: 的外部,则直线
的外部,则直线 与圆C的位置关系是( )
与圆C的位置关系是( )
| A.相切 | B.相离 | C.相交 | D.相交或相切 |
 和圆
和圆 ,圆心为M,点
,圆心为M,点 在直线
在直线 上,若圆
上,若圆 与直线
与直线 至少有一个公共点
至少有一个公共点 ,且
,且 ,则点
,则点

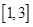

 与圆
与圆 相交于
相交于 两点(其中
两点(其中 是实数),且
是实数),且 是直角三角形(
是直角三角形( 是坐标原点),则点
是坐标原点),则点
 与点
与点
 之间距离的最大值为 ( )
之间距离的最大值为 ( )


