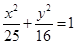题目内容
圆 上的点到直线
上的点到直线 距离的最大值是( )
距离的最大值是( )
A. | B. | C. | D. |
B
解析试题分析:圆 上的点到直线
上的点到直线 距离的最大值为圆心(1,1)到直线的距离加上半径1,所以距离的最大值为
距离的最大值为圆心(1,1)到直线的距离加上半径1,所以距离的最大值为 再加上半径1,所以距离的最大值为
再加上半径1,所以距离的最大值为 .
.
考点:本小题主要考查直线与圆的位置关系.
点评:解决本小题关键是看出所求的最大距离为圆心到直线的距离加上圆半径,进而利用点到直线的距离公式解决题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若关于 的方程组
的方程组 有实数解,则实数
有实数解,则实数 满足( )
满足( )
A. | B. | C. | D. |
圆 关于直线
关于直线 对称的圆的方程是( )
对称的圆的方程是( )
A. | B. |
C. | D. |
直线过点P(0,2),且截圆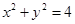 所得的弦长为2,则直线的斜率为
所得的弦长为2,则直线的斜率为
A.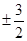 | B.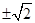 | C.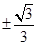 | D.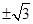 |
若圆 的圆心到直线
的圆心到直线 的距离为
的距离为 ,则
,则 的值为( )
的值为( )
A. 或 或 | B. 或 或 | C. 或 或 | D. 或 或 |
若圆 的半径为1,圆心在第一象限,且与直线
的半径为1,圆心在第一象限,且与直线 和
和 轴相切,则该圆的标准方程是( )
轴相切,则该圆的标准方程是( )
A. | B. |
C. | D. |
已知两点 ,点
,点 是圆
是圆 上任意一点,则
上任意一点,则 面积的最小值是( ).
面积的最小值是( ).
A. | B. | C. | D. |
直线 与椭圆
与椭圆 交于
交于 两点,以线段
两点,以线段 为直径的圆过椭圆的右焦点,则椭圆
为直径的圆过椭圆的右焦点,则椭圆 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
 和点B(3,0),P是圆上一点,线段BP的垂直平分线交CP于M点,则M点的轨迹方程是( )。
和点B(3,0),P是圆上一点,线段BP的垂直平分线交CP于M点,则M点的轨迹方程是( )。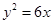 .
.