题目内容
求椭圆 x2+49y2=49的长轴长、短轴长、焦距、离心率、焦点坐标及顶点坐标．
解：∵椭圆 x2+49y2=49即
∴a=7，b=1
由 c2=a2-b2，得c=4
长轴长：2a=14
短轴长：2b=2
焦距：2c=8
离心率：e=
=
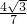
焦点坐标：F1（-4，0），F2（4，0）
顶点坐标：（7，0），（-7，0），（0，1），（0，-1
分析：首先将椭圆方程化成标准方程，能够得出a=7，b=1，c=4，然后根据各自的公式求出结果即可．
点评：本题考查了椭圆的性质，求出a、b、c是关键，同时要牢记椭圆的有关公式，属于基础题．
∴a=7，b=1
由 c2=a2-b2，得c=4
长轴长：2a=14
短轴长：2b=2
焦距：2c=8
离心率：e=
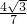
=焦点坐标：F1（-4
，0），F2（4，0）顶点坐标：（7，0），（-7，0），（0，1），（0，-1
分析：首先将椭圆方程化成标准方程，能够得出a=7，b=1，c=4
，然后根据各自的公式求出结果即可．点评：本题考查了椭圆的性质，求出a、b、c是关键，同时要牢记椭圆的有关公式，属于基础题．
练习册系列答案
相关题目