题目内容
已知（2x+1）5=a5x5+a4x4+…+a1x+a0，则a5+a4+…+a1= ．
考点：二项式系数的性质
专题：排列组合
分析：根据展开式的特点，利用赋值法，分别令x=0，1求出即可．
解答：
解：在（2x+1）5=a5x5+a4x4+…+a1x+a0中，
令x=0得，a0=1，令x=1得，a5+a4+…+a1+a0=（2×1+1）5=243，
所以a5+a4+…+a1=242．
故答案为：242．
令x=0得，a0=1，令x=1得，a5+a4+…+a1+a0=（2×1+1）5=243，
所以a5+a4+…+a1=242．
故答案为：242．
点评：本题考查二项式定理的应用，着重考查导数法与赋值法的应用，属于中档题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
如图所示，点A，B是圆O上的两点，∠AOB=120°，点D是圆周上异于A，B的任意一点，线段OD与线段AB交于点C．若
如图，抛物线y=-x2+2（m+1）x+m+3与x轴交于A、B两点，且OA：OB=3：1，则m=若角α、β的终边关于y轴对称，则下列等式成立的是（ ）
| A、sinα=sinβ |
| B、cosα=cosβ |
| C、tanα=tanβ |
| D、cotα=cotβ |
以下是解决数学问题的思维过程的流程图：
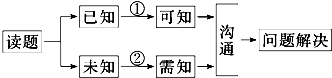
在此流程图中，①②两条流程线与“推理与证明”中的思维方法匹配正确的是（ ）
在此流程图中，①②两条流程线与“推理与证明”中的思维方法匹配正确的是（ ）
| A、①-综合法，②-分析法 |
| B、①-分析法，②-综合法 |
| C、①-综合法，②-反证法 |
| D、①-分析法，②-反证法 |
若函数f（x）=
x3+atanx-bx+
，且f（1）=-1，则f（-1）=（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |