题目内容
如图所示，四面体ABCD被一平面所截，截面与四条棱AB、AC、CD、BD相交于E、F、G、H四点，且截面EFGH是一个平行四边形.求证：棱BC∥平面EFGH，AD∥平面EFGH.
解析：依据判定定理，在平面EFGH内寻找与BC、AD平行的直线，利用线面平行的性质即得.
证明：因为截面EFGH是一个平行四边形，所以EF∥GH.
又因为GH在平面DCB内，EF不在平面DCB内，所以EF∥平面DCB.
又平面ABC过直线EF且与平面DCB相交于BC.
所以EF∥BC，EF
平面EFGH.所以BC∥平面EFGH.
同理，可证AD∥平面EFGH.
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
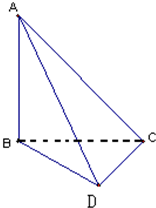在如图所示的四面体ABCD中，AB、BC、CD两两互相垂直，且BC=CD=1．
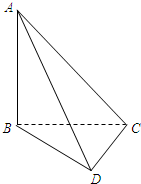（2009•襄阳模拟）在如图所示的四面体ABCD中，AB、BC、CD两两互相垂直，且BC=CD=1．
（2009•河东区二模）如图所示，四面体ABCD中，O、E分别是BD和BC的中点，且
