题目内容
已知a,b∈R且a≠2,定义在区间(-b,b)内的函数 是奇函数。
是奇函数。
(Ⅰ)求函数f(x)的解析式及b的取值范围;
(Ⅱ)讨论f(x)的单调性。
 是奇函数。
是奇函数。(Ⅰ)求函数f(x)的解析式及b的取值范围;
(Ⅱ)讨论f(x)的单调性。
解:(Ⅰ)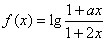 ,
,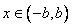 是奇函数,
是奇函数,
等价于对于任意-b<x<b都有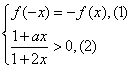 成立,
成立,
(1)式即为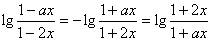 ,
,
∴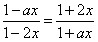 ,即
,即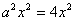 ,
,
此式对于任意x∈(-b,b)都成立等价于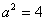 ,
,
因为a≠2,所以a=-2,
所以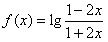 ;
;
代入(2)式得: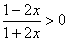 ,即
,即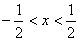 ,
,
对于任意x∈(-b,b)都成立,相当于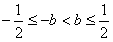 ,
,
从而,b的取值范围为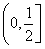 ;
;
(Ⅱ)对于任意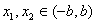 ,且
,且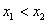 ,
,
由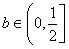 ,得
,得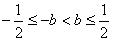 ,
,
所以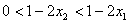 ,
,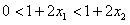 ,
,
从而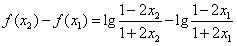
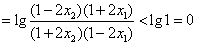 ,
,
因此,f(x)在(-b,b)是减函数。
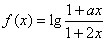 ,
,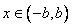 是奇函数,
是奇函数,等价于对于任意-b<x<b都有
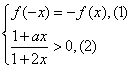 成立,
成立,(1)式即为
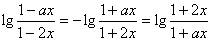 ,
,∴
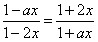 ,即
,即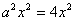 ,
,此式对于任意x∈(-b,b)都成立等价于
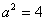 ,
,因为a≠2,所以a=-2,
所以
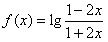 ;
;代入(2)式得:
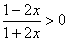 ,即
,即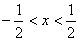 ,
,对于任意x∈(-b,b)都成立,相当于
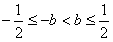 ,
,从而,b的取值范围为
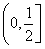 ;
;(Ⅱ)对于任意
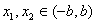 ,且
,且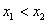 ,
,由
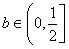 ,得
,得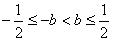 ,
,所以
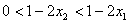 ,
,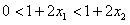 ,
,从而
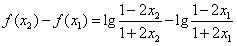
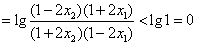 ,
,因此,f(x)在(-b,b)是减函数。

练习册系列答案
相关题目