题目内容
用秦九韶算法求n次多项式f（x）=anxn+an-1xn-1+…+a1x的值，当x=2时，求f（2）需用乘法运算 次，加法运算 次．
考点：秦九韶算法
专题：算法和程序框图
分析：由秦九韶算法可得n次多项式f（x）=anxn+an-1xn-1+…+a1x=（…（anx+an-1）x+an-2）x+…+a1）x，即可得出．
解答：
解：由秦九韶算法可得n次多项式f（x）=anxn+an-1xn-1+…+a1x=（…（anx+an-1）x+an-2）x+…+a1）x，
当x=2时，求f（2）需用乘法运算 n次，加法运算 n-1次．
故答案分别为：n，n-1．
当x=2时，求f（2）需用乘法运算 n次，加法运算 n-1次．
故答案分别为：n，n-1．
点评：本题考查了秦九韶算法，属于基础题．
练习册系列答案
相关题目
若全集U=Z，集合A={n|
∈z}，集合B={n|
∈z}，则A∩{CuB}是（ ）
| n |
| 2 |
| n |
| 3 |
| A、{n|n=3k+1，k∈z} |
| B、{n|n=4k或n=4k+2，k∈z} |
| C、{n|n=6k±1，k∈z} |
| D、{n|n=6k±2，k∈z} |
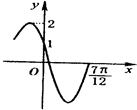
如图是函数f（x）=Asin（ωx+φ）（A＞0，0＜ω＜3，0＜φ＜π）的图象的一部分，则ωφ=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）=
，若|f（x）|≥2m，则m的取值范围是（ ）
|
| A、[-2，0] |
| B、（-∞，0] |
| C、[-2，1] |
| D、[-1，0] |