题目内容
1.若$\sqrt{{x}^{2}-8x+16}$=x-4,则实数x的取值范围是[4,+∞).分析 把根式内部的代数式化为完全平方数的形式,开方后由绝对值的性质得答案.
解答 解:∵$\sqrt{{x}^{2}-8x+16}$=$\sqrt{(x-4)^{2}}=|x-4|=x-4$,
∴x-4≥0,即x≥4.
∴实数x的取值范围是[4,+∞).
故答案为:[4,+∞).
点评 本题考查根式与分数指数幂的互化及运算,考查了绝对值的去法,是基础题.

练习册系列答案
相关题目
16.直线a和面α所成角为60°,b?α,则a,b所成角的范围是( )
| A. | [0°,90°] | B. | [30°,90°] | C. | [60°,90°] | D. | [60°,120°] |
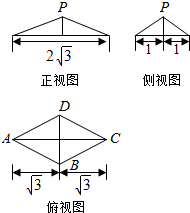 已知四棱锥P-ABCD的三视图如图所示,其中俯视图是菱形,正视图和侧视图都是等腰三角形,已知M为BC上一点,且BM=$\frac{1}{2}$,PA⊥PM.
已知四棱锥P-ABCD的三视图如图所示,其中俯视图是菱形,正视图和侧视图都是等腰三角形,已知M为BC上一点,且BM=$\frac{1}{2}$,PA⊥PM.