题目内容
【题目】在平面直角坐标系中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρ2﹣6ρcosθ+5=0,曲线C2的参数方程为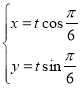 (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程,并说明是什么曲线?
(2)若曲线C1与C2相交于A、B两点,求|AB|的值.
【答案】(1)(x﹣3)2+y2=4,曲线C1是以(3,0)为圆心,以2为半径的圆;(2)![]()
【解析】
(1)把![]() ,代入
,代入![]() ,即可求得曲线C1的直角坐标方程,配方可得曲线C1是以
,即可求得曲线C1的直角坐标方程,配方可得曲线C1是以![]() 为圆心,以2为半径的圆;(2)由已知可得,曲线C2过定点
为圆心,以2为半径的圆;(2)由已知可得,曲线C2过定点![]() ,倾斜角为
,倾斜角为![]() 的直线,把其方程代入圆的方程,联立后利用参数
的直线,把其方程代入圆的方程,联立后利用参数![]() 的几何意义求解.
的几何意义求解.
(1)![]() ,代入
,代入![]() ,
,
可得![]() .
.
∴曲线C1的直角坐标方程为![]() ,
,
即![]() ,
,
曲线C1是以(3,0)为圆心,以2为半径的圆;
(2)由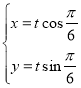 ,即
,即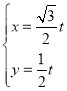 ,可知曲线C2过定点
,可知曲线C2过定点![]() ,倾斜角为
,倾斜角为![]() ,
,
把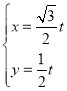 代入
代入![]() ,可得
,可得![]() .
.
则![]() ,t1t2=5.
,t1t2=5.
![]() .
.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案【题目】某企业为确定下一年度投入某种产品的生产所需的资金,需了解每投入2千万资金后,工人人数![]() (单位:百人)对年产能
(单位:百人)对年产能![]() (单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
(单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

(1)根据散点图判断:![]() 与
与![]() 哪一个适宜作为年产能
哪一个适宜作为年产能![]() 关于投入的人力
关于投入的人力![]() 的回归方程类型?并说明理由?
的回归方程类型?并说明理由?
(2)根据(1)的判断结果及相关的计算数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)现该企业共有2000名生产工人,资金非常充足,为了使得年产能达到最大值,则下一年度共需投入多少资金(单位:千万元)?
附注:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为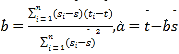 ,(说明:
,(说明:![]() 的导函数为
的导函数为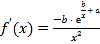 )
)
【题目】在某市高中某学科竞赛中,某一个区4000名考生的参赛成绩统计如图所示.
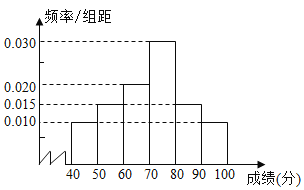
(1)求这4000名考生的竞赛平均成绩![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)记70分以上为优秀,70分及以下为合格,结合频率分布直方图完成下表,并判断是否有99%的把握认为该学科竞赛成绩与性别有关?
合格 | 优秀 | 合计 | |
男生 | 720 |
|
|
女生 |
| 1020 |
|
合计 |
|
| 4000 |
附:
p(k2≥k0) | 0.010 | 0.005 | 0.001 |
k0 | 6.635 | 7.879 | 10.828 |
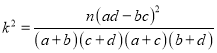 .
.