题目内容
(本小题满分14分)
某工厂的A、B、C三个不同车间生产同一产品的数量(单位:件)如下表所示. 质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测.
车间 | A | B | C |
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自A、B、C各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件商品来自相同车间的概率.
(1)来自A、B、C各车间产品的数量分别为1,3,2;(2) .
.
【解析】
试题分析:(1)确定抽样比例即可求出;(2)先确定在这6件样品中随机抽取2件的基本事件总数,再确定2件商品来自相同车间的基本事件的个数,利用古典概型求概率公式即可求出.
试题解析:【解析】
(1)因为样本容量与总体中的个体数的比是 ,(3分)
,(3分)
所以A车间产品被选取的件数为 , (4分)
, (4分)
B车间产品被选取的件数为 , (5分)
, (5分)
C车间产品被选取的件数为 . (6分)
. (6分)
(2)设6件来自A、B、C三个车间的样品分别为:A;B1,B2,B3;C1,C2.
则从6件样品中抽取的这2件产品构成的所有基本事件为:(A,B1),(A,B2),(A,B3),(A,C1),(A,C2),(B1,B2),(B1,B3),(B1,C1),(B1,C2),(B2,B3),(B2,C1),(B2,C2),(B3,C1),(B3,C2),(C1,C2),共15个. (10分)
每个样品被抽到的机会均等,因此这些基本事件的出现是等可能的. 记事件D:“抽取的这2件产品来自相同车间”,则事件D包含的基本事件有:(B1,B2),(B1,B3),(B2,B3),(C1,C2),共4个. (12分)
所以 ,即这2件产品来自相同车间的概率为
,即这2件产品来自相同车间的概率为 . (14分)
. (14分)
考点:1、分层抽样;2、古典概率模型.

 ”的单调递增函数是( )
”的单调递增函数是( ) B.
B. C.
C. D.
D.
 中,已知
中,已知 ,则该数列前11项和
,则该数列前11项和 等于( )
等于( )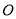 和不共线的三点
和不共线的三点 、
、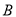 、
、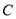 有
有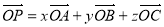 ,则
,则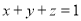 是四点
是四点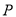 、
、 中,已知
中,已知 ,则该数列前11项和
,则该数列前11项和 等于( )
等于( ) 与
与
 与
与
 与
与
 与
与
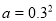 ,
, ,
,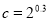 之间的大小关系是( )
之间的大小关系是( )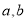 与平面
与平面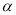 ,则下列四个命题中假命题是
,则下列四个命题中假命题是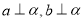 ,那么
,那么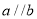 B.如果
B.如果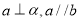 ,那么
,那么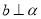
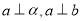 ,那么
,那么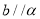 D.如果
D.如果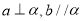 ,那么
,那么