题目内容
已知函数 (
( 为实数,
为实数, ,
, ),
),
(1)若 ,且函数
,且函数 的值域为
的值域为 ,求
,求 的表达式;
的表达式;
(2)在(1)的条件下,当 时,
时, 是单调函数,求实数
是单调函数,求实数 的取值范围;
的取值范围;
(3)设 ,
, ,
, ,且函数
,且函数 为偶函数,判断
为偶函数,判断 是否大于
是否大于 ?
?
【答案】
解:(Ⅰ)因为 ,所以
,所以 .
.
因为 的值域为
的值域为 ,所以
,所以 ……… 2分
……… 2分
所以 .解得
.解得 ,
, .所以
.所以 .
.
所以 ………… 4分
………… 4分
(Ⅱ)因为
= , ……… 6分
, ……… 6分
所以当  或
或 时
时 单调.
单调.
即 的范围是
的范围是 或
或 时,
时, 是单调函数. … 8分
是单调函数. … 8分
(Ⅲ)因为 为偶函数,所以
为偶函数,所以 .
.
所以 …………… 10分
…………… 10分
因为 , 依条件设
, 依条件设 ,则
,则 .
.
又 ,所以
,所以 .
.
所以 .
……………… 12分
.
……………… 12分
此时
 .
.
即 .
.
【解析】略

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 (
( 为实数).
为实数). 时,
求
时,
求 的最小值;
的最小值; 上是单调函数,求
上是单调函数,求 (
( 为实数).
为实数). 时,
求
时,
求 的最小值;
的最小值; 上是单调函数,求
上是单调函数,求 (
( 为实数,
为实数,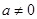 ,
, ).
). 的图像过点
的图像过点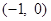 ,且方程
,且方程 有且只有一个根,求
有且只有一个根,求 当
当 ,
, ,
, ,且函数
,且函数 能否大于
能否大于 ?
?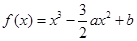 (
( 为实数,且
为实数,且 ),在区间
),在区间 上最大值为
上最大值为 ,最小值为
,最小值为
 的解析式
的解析式 在区间
在区间 上为减函数,求实数
上为减函数,求实数 的取值范围
的取值范围 作函数
作函数 图象的切线,求切线方程
图象的切线,求切线方程