题目内容
已知公差大于零的等差数列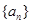 的前n项和为
的前n项和为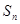 ,且满足:
,且满足: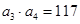 ,
,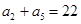 .
.
(1)求数列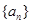 的通项公式
的通项公式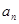 ;
;
(2)若数列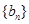 是等差数列,且
是等差数列,且 ,求非零常数c;
,求非零常数c;
(3)在(2)的条件下,设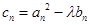 ,已知数列
,已知数列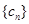 为递增数列,求实数
为递增数列,求实数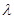 的取值范围.
的取值范围.
(1) (2)
(2) (3)
(3)
解析试题分析:解:(1)由 得,
得,
解得 或
或
因为等差数列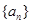 的公差大于零,所以
的公差大于零,所以
由 解得
解得
所以
(2)由(1)得:
所以
由 成等差数列得
成等差数列得
列示得 ,解得
,解得

(3) ,由
,由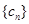 为递增数列,得
为递增数列,得
得 分离参数得
分离参数得 ,又
,又 在n=1时取得最小值12
在n=1时取得最小值12
考点:等差数列的通项公式
点评:在等差数列中,当涉及到两项相加(像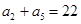 ),常用到性质:
),常用到性质:
,而在等比数列中,若涉及到两项相乘,则常用到性质: 。另外,数列的定义很重要,像本题第二小题就用到等差数列的定义,结合数列的定义还可以证明一个数列是什么数列。
。另外,数列的定义很重要,像本题第二小题就用到等差数列的定义,结合数列的定义还可以证明一个数列是什么数列。

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 中,
中,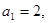 且
且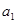 ,
,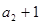 ,
,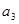 成等差数列,
成等差数列,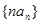 的前
的前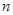 项的和.
项的和.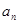 }的前
}的前 项和为
项和为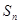 ,已知
,已知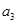 =
= ,
,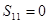 .
.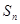 ;
;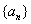 中,
中, 为前n项和,且满足
为前n项和,且满足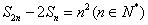
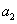 及数列
及数列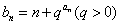 ,求数列
,求数列 的前n项和
的前n项和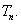
 }是等差数列,其前
}是等差数列,其前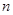 项和为
项和为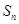 ,{
,{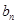 }是等比数列,且
}是等比数列,且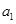 =
=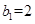 ,
,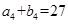 ,
,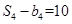 .
.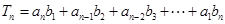 ,求满足不等式
,求满足不等式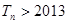 的最小正整数
的最小正整数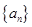 的前四项和为10,且
的前四项和为10,且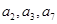 成等比数列
成等比数列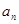
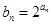 ,求数列
,求数列 的前
的前 项和
项和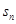
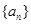 是等差数列,其中
是等差数列,其中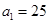 ,
,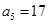 。
。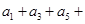 …
…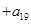 的值。
的值。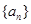 的各项均为正数,
的各项均为正数,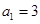 ,前
,前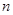 项和为
项和为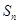 ,
,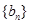 为等比数列,
为等比数列, 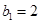 ,且
,且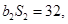
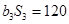 .
.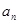 与
与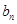 ;
;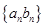 的前
的前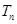 。
。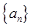 的公差
的公差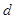 =1,前
=1,前 项和为
项和为 .
.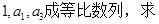
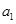 ;
;