题目内容
(本题满分12分)
等差数列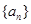 的各项均为正数,
的各项均为正数,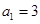 ,前
,前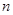 项和为
项和为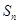 ,
,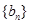 为等比数列,
为等比数列, 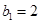 ,且
,且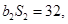
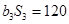 .
.
(1)求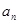 与
与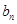 ;
;
(2)求数列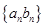 的前
的前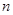 项和
项和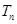 。
。
(1)  (1)
(1) 
解析试题分析:(1)设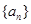 的公差为
的公差为 ,
,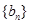 的公比为
的公比为 ,则
,则 为正整数,
为正整数, ,
,
依题意有 ,即
,即 ,
,
解得 或者
或者 (舍去),
(舍去),
故 。
。
(2) 。
。 ,
, ,
,
两式相减得
 ,
,
所以 。
。
考点:等差数列和等比数列
点评:解决的关键是能根据错位相减法来准确的求解数列的和,易错点是对于项数的准确求解,属于基础题。

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
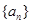 的前n项和为
的前n项和为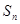 ,且满足:
,且满足: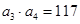 ,
,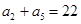 .
.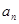 ;
;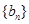 是等差数列,且
是等差数列,且 ,求非零常数c;
,求非零常数c;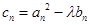 ,已知数列
,已知数列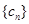 为递增数列,求实数
为递增数列,求实数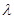 的取值范围.
的取值范围. 的公差大于0,且
的公差大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前n项的和为
的前n项的和为 ,且
,且 (
( ).
). ,求证:
,求证: .
. 满足:
满足: ,
, ,
,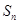 .
. 及
及 (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和 .
.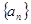 的公差
的公差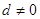 ,
, 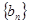 是等比数列,又
是等比数列,又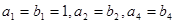
 。
。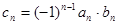 ,求数列
,求数列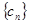 的前
的前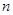 项和
项和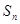 。
。 满足:
满足: ,
, ,
, .
. 及
及 (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和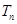 .
.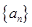 的前
的前 项和记为
项和记为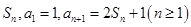
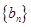 的各项为正,其前
的各项为正,其前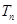 ,且
,且 ,又
,又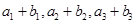 成等比数列,求
成等比数列,求 满足:
满足: ,
, .
. .
. 及
及 ;
; ,
, (
(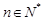 ),求数列
),求数列 的前
的前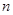 项和
项和 .
. 的前
的前 项和
项和 。
。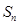 的最大或最小值。
的最大或最小值。