题目内容
将函数y=sin(x+ )的图象上各点的横坐标伸长到原来的2倍,所得图象的函数解析式是
)的图象上各点的横坐标伸长到原来的2倍,所得图象的函数解析式是
- A.y=cosx
- B.y=sin(2x+
 )
) - C.y=sin(
 x+
x+ )
) - D.y=sin(
 +
+ )
)
D
分析:函数y=sin(x+ )的图象上各点纵坐标不变,说明最大值仍然是1,故振幅不变;横坐标伸长到原来的2倍,说明周期变成原来的2倍,由三角函数的周期公式得后来函数的x的系数变成
)的图象上各点纵坐标不变,说明最大值仍然是1,故振幅不变;横坐标伸长到原来的2倍,说明周期变成原来的2倍,由三角函数的周期公式得后来函数的x的系数变成 ;再根据函数零点(-
;再根据函数零点(- ,0)变成点(
,0)变成点( ,0),可得初相为
,0),可得初相为 也不变,由此正确的选项.
也不变,由此正确的选项.
解答:∵函数y=sin(x+ )的图象横坐标伸长,而纵坐标不变
)的图象横坐标伸长,而纵坐标不变
∴函数的振幅不变,仍为1,
由三角函数周期的公式,得到数y=sin(x+ )的周期为T=
)的周期为T=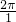 =2π
=2π
∵将函数y=sin(x+ )的图象上各点的横坐标伸长到原来的2倍,
)的图象上各点的横坐标伸长到原来的2倍,
∴横坐标伸长后,所得函数的周期为T1=2π×2=4π
因此横坐标伸长后所得函数的x的系数变成 ,
,
∴可设变换的函数解析式为y=sin( x+φ)
x+φ)
又∵变换前函数的零点(- ,0)变成点(
,0)变成点( ,0),
,0),
∴变换后的初相φ=
∴所得图象的函数解析式是y=sin( +
+ )
)
故选D
点评:本题借助于一个三角函数图象的变换为例,着重考查了三角函数的周期、振幅和初相等概念和有关公式,属于基础题.
分析:函数y=sin(x+
 )的图象上各点纵坐标不变,说明最大值仍然是1,故振幅不变;横坐标伸长到原来的2倍,说明周期变成原来的2倍,由三角函数的周期公式得后来函数的x的系数变成
)的图象上各点纵坐标不变,说明最大值仍然是1,故振幅不变;横坐标伸长到原来的2倍,说明周期变成原来的2倍,由三角函数的周期公式得后来函数的x的系数变成 ;再根据函数零点(-
;再根据函数零点(- ,0)变成点(
,0)变成点( ,0),可得初相为
,0),可得初相为 也不变,由此正确的选项.
也不变,由此正确的选项.解答:∵函数y=sin(x+
 )的图象横坐标伸长,而纵坐标不变
)的图象横坐标伸长,而纵坐标不变∴函数的振幅不变,仍为1,
由三角函数周期的公式,得到数y=sin(x+
 )的周期为T=
)的周期为T=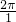 =2π
=2π∵将函数y=sin(x+
 )的图象上各点的横坐标伸长到原来的2倍,
)的图象上各点的横坐标伸长到原来的2倍,∴横坐标伸长后,所得函数的周期为T1=2π×2=4π
因此横坐标伸长后所得函数的x的系数变成
 ,
,∴可设变换的函数解析式为y=sin(
 x+φ)
x+φ)又∵变换前函数的零点(-
 ,0)变成点(
,0)变成点( ,0),
,0),∴变换后的初相φ=

∴所得图象的函数解析式是y=sin(
 +
+ )
)故选D
点评:本题借助于一个三角函数图象的变换为例,着重考查了三角函数的周期、振幅和初相等概念和有关公式,属于基础题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
将函数y=sin(x-θ)的图象F向右平移
个单位长度得到图象F′,若F′的一条对称轴是直线x=
则θ的一个可能取值是( )
| π |
| 3 |
| π |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
将函数y=sin(x+φ)的图象F向左平移
个单位长度后得到图象F′,若F′的一个对称中心为(
,0),则φ的一个可能取值是( )
| π |
| 6 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|