Question

【题目】已知向量m＝(3sinx，cosx)，n＝(－cosx， cosx)，f(x)＝m·n－.

(1)求函数f(x)的最大值及取得最大值时x的值；

(2)若方程f(x)＝a在区间上有两个不同的实数根，求实数a的取值范围．

Answer 1

【答案】（1）；（2）．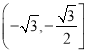

【解析】试题分析：（1）根据向量的数量积运算，化简得到

，根据三角函数的性质求出最值，
（2）求出函数 的单调区间，并画出 ）和 的图象，由图象可得到答案．

试题解析：(1)f(x)＝m·n－＝－3sinxcosx＋cos2x－＝－sin2x＋ (1＋cos2x)－

＝－sin2x＋cos2x＝sin.

当2x＋＝2kπ＋，即x＝kπ－，k∈Z时，函数f(x)取得最大值.

(2)由于x∈时，2x＋∈.

而函数g(x)＝sinx在区间上单调递减，在区间上单调递增．

又g＝－，g＝－，g＝.

所以方程f(x)＝a在区间上有两个不同的实数根时，a∈.