题目内容
已知平面 平面
平面 ,四边形
,四边形 是矩形,
是矩形, ,
,  、
、 分别是
分别是 、
、 的中点,主(正)视图方向垂直平面
的中点,主(正)视图方向垂直平面 时,左(侧)视图的面积为
时,左(侧)视图的面积为 .
.
 ⑴求证:
⑴求证: ∥平面
∥平面 ;
;
⑵求证:平面
 平面
平面 .
.
⑴证明:方法一、取 的中点
的中点 ,连接
,连接 ,
,
 因为
因为 中,
中, 、
、 分别是
分别是 、
、 的中点,
的中点,
所以 ∥
∥ 且
且 =
=
 ;……………………1分
;……………………1分
因为矩形 中,
中, 是
是 的中点,
的中点, ∥
∥ 且
且 =
=
 ;
;
所以 ∥
∥ 且
且 =
= ,得平行四边形
,得平行四边形 ,
, ∥
∥ ……2分
……2分
因为
 平面
平面 ,
,
 平面
平面 ,所以
,所以 ∥平面
∥平面 ;……4分
;……4分
方法一、取 的中点
的中点 ,连接
,连接 、
、 ,
,
因为 中,
中, 、
、 分别是
分别是 、
、 的中点,所以
的中点,所以 ∥
∥ ,
,
因为
 平面
平面 ,
, 
 平面
平面 ,所以
,所以 ∥平面
∥平面 ;………1分
;………1分
同理可证 ∥平面
∥平面 ;………………………………………………2分
;………………………………………………2分
因为

 =
= ,所以平面
,所以平面 ∥平面
∥平面 ;…………………3分
;…………………3分
 因为
因为
 平面
平面 ,所以
,所以 ∥平面
∥平面 ;……………………4分
;……………………4分
⑵证明:取 中点
中点 ,连接
,连接 、
、 、
、 ,
,
则矩形 中,
中, ,
, ,………………5分
,………………5分
因为 中
中 ,所以
,所以 ,
,
因为平面 平面
平面 ,交线为
,交线为 ,所以
,所以 平面
平面 ,
, ,
,
所以 的面积等于几何体
的面积等于几何体 左(侧)视图的面积,得
左(侧)视图的面积,得
 即
即 ;…………………8分
;…………………8分
所以 中,
中, ,
, ,
,
 ,
, ,
, ;……………………10分
;……………………10分
因为平面 平面
平面 ,四边形
,四边形 是矩形,所以
是矩形,所以 平面
平面 ,
,
因为 平面
平面 ,所以
,所以 ;……………………11分
;……………………11分
因为 ,所以
,所以 平面
平面 ;…………………12分
;…………………12分
因为 平面
平面 ,所以平面
,所以平面
 平面
平面 . ……………………13分
. ……………………13分

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 ,
, ,若
,若 ,求
,求 的值.
的值. 的定义域是
的定义域是 ,则函数
,则函数 的定义域是
的定义域是
 的立方体表面涂上红色后,再均匀分割成棱长为1
的立方体表面涂上红色后,再均匀分割成棱长为1 的概率是( )
的概率是( ) .
.
 .
. .
.
 .
.
 ,
, ,
, ,其中
,其中 是圆周率,
是圆周率, …是自然对数的底数,则输出的结果是 .
…是自然对数的底数,则输出的结果是 . 
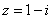 (
(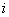 是虚数单位),则复数
是虚数单位),则复数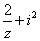 的虚部是( )
的虚部是( )  B.
B.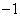 C.
C.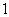
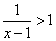 的解集为 .
的解集为 . 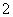 的正方形
的正方形 内部任取一点
内部任取一点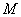 ,则满足
,则满足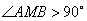 的概率为_______.
的概率为_______.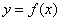 为奇函数,且对定义域内的任意x都有
为奇函数,且对定义域内的任意x都有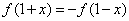 .当
.当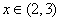 时,
时,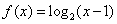
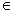 Z)成中心对称;
Z)成中心对称; 是以2为周期的周期函数;
是以2为周期的周期函数; 时,
时,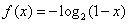 ;
;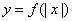 在(k,k+1)( k
在(k,k+1)( k