题目内容
已知数列{an}满足a
=a
+4,且a1=1,an>0,则an= .
|
|
考点:数列递推式
专题:等差数列与等比数列
分析:根据条件构造等差数列,即可得到结论.
解答:
解:∵a
=a
+4,
∴a
-a
=4,
故数列{an2}是以a12=1为首项,公差d=4的等差数列,
则an2=1+4(n-1)=4n-3,
则an=
,
故答案为:
|
|
∴a
|
|
故数列{an2}是以a12=1为首项,公差d=4的等差数列,
则an2=1+4(n-1)=4n-3,
则an=
| 4n-3 |
故答案为:
| 4n-3 |
点评:本题主要考查数列通项公式的应用,根据条件构造等差数列是解决本题的关键.

练习册系列答案
相关题目
已知a,b为正数,且满足2<a+2b<4,那么3a-b的取值范围是( )
| A、(-4,6) |
| B、(-2,6) |
| C、(-4,12) |
| D、(-2,12) |
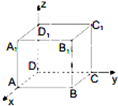 如图,把棱长为2的正方体ABCD-A1B1C1D1放在空间直角坐标系中,使D与原点重合,点A与点C分别放在x轴和y轴的正半轴上,则B1的坐标为:( )
如图,把棱长为2的正方体ABCD-A1B1C1D1放在空间直角坐标系中,使D与原点重合,点A与点C分别放在x轴和y轴的正半轴上,则B1的坐标为:( )| A、(2,2,2) |
| B、(2,2,0) |
| C、(2,0,2) |
| D、(0,2,2) |
 如图所示曲线是幂函数y=xa在第一象限内的图象,其中a=±
如图所示曲线是幂函数y=xa在第一象限内的图象,其中a=±| 1 |
| 2 |
A、
| ||||
B、2、
| ||||
C、-
| ||||
D、2、
|
设i是虚数单位,则复数z=i(-2+i)的虚部为( )
| A、-2 | B、-1 | C、-2i | D、2i |