题目内容
在平面直角坐标系xOy中,设中心在坐标原点的椭圆C的左、右焦点分别为F1、F2,右准线
l:x=m+1与x轴的交点为B,BF2=m.
(1)已知点(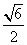 ,1)在椭圆C上,求实数m的值;
,1)在椭圆C上,求实数m的值;
(2)已知定点A(-2,0).
①若椭圆C上存在点T,使得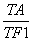 =
=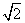 ,求椭圆C的离心率的取值范围;
,求椭圆C的离心率的取值范围;
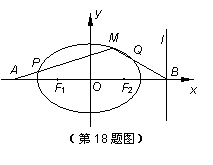
②当m=1时,记M为椭圆C上的动点,直线AM,BM分别与椭圆C交于另一点P,Q,
若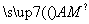 =λ
=λ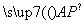 ,
,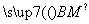 =
= ,求证:λ+为定值.
,求证:λ+为定值.
 |
解:(1)设椭圆C的方程为 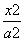 +
+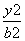 =1(a>b>0).
=1(a>b>0).
 解得m=2或m=-
解得m=2或m=-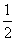 (舍去).
(舍去).
所以m=2.
(2)①设点T(x,y).
由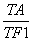 =
=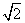 ,得(x+2)2+y2=2[(x+1)2+y2],即x2+y2=2.
,得(x+2)2+y2=2[(x+1)2+y2],即x2+y2=2.
由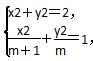 得y2=m2-m.
得y2=m2-m.
因此0≤m2-m≤m,解得1≤m≤2.
 即2(
即2(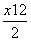 +y12)+2(-1)x1+2(-1)2-1=0.
+y12)+2(-1)x1+2(-1)2-1=0.
因为 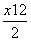 +y12=1,代入得2 (-1)x1+32-4+1=0.
+y12=1,代入得2 (-1)x1+32-4+1=0.
由题意知,≠1,
故x1=-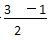 ,所以x0=
,所以x0=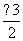 .
.
同理可得x0=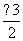 .
.
因此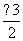 =
=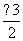 ,
,
所以+=6.
(方法二)设M(x0,y0),P(x1,y1),Q(x2,y2).
 即λ+为定值6.
即λ+为定值6.

练习册系列答案
相关题目
 在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上是________
在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上是________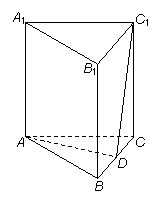 (2)设E是B1C1上的一点,当
(2)设E是B1C1上的一点,当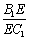 的值为多少时,A1E∥平面ADC1?请给出证明.
的值为多少时,A1E∥平面ADC1?请给出证明. A”是“x
A”是“x (∈R)交于A,B两点,求以AB为直径的圆的极坐标方程.
(∈R)交于A,B两点,求以AB为直径的圆的极坐标方程. 中,抛物线
中,抛物线 上横坐标为1的点到其焦点的距离为 .
上横坐标为1的点到其焦点的距离为 . ,
, ,
, ,则
,则 为( )
为( )  B.
B.  C.
C.  D.
D. 

 上给定曲线
上给定曲线

 时,求
时,求 值.
值.
 的值,使图中所给阴影部分的面积
的值,使图中所给阴影部分的面积
 与
与
 之和最小.
之和最小.