题目内容
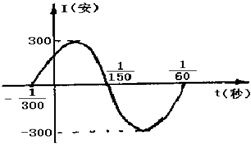 如图电流强度I与时间t的关系式I=Asin(ωx+φ)(A>0,ω>0,-
如图电流强度I与时间t的关系式I=Asin(ωx+φ)(A>0,ω>0,-| π |
| 2 |
| π |
| 2 |
(1)求函数的解析式;
(2)求函数的单调减区间;
(3)为了使I=Asin(ωx+φ)中t在任意一段
| 1 |
| 50 |
分析:(1)由图象的顶点纵坐标求出A,由周期求出ω,根据五点法作图求出∅.
(2)由 2kπ+
≤100πt +
≤2kπ+
,求出x的范围,即为函数的减区间.
(3)要使t在任意一段
秒能取得最大值和最小值,必须使得周期T≤
,解不等式求得ω的范围,从而得到ω的最小值.
(2)由 2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
(3)要使t在任意一段
| 1 |
| 50 |
| 1 |
| 50 |
解答:解:(1)由图可知:A=300,周期T=
-(-
)=
;由
=T?ω=
=100π;
当t=-
时,ωt+φ=0,即φ=-ωt=-100π•(-
)=
;
故图象的解析式为:I=300sin(100πt+
).
(2)由 2kπ+
≤100πt +
≤2kπ+
,k∈z,可得
+
≤x≤
+
,k∈Z,
故函数的减区间为 [
+
,
+
],k∈Z.
(3)要使t在任意一段
秒能取得最大值和最小值,必须使得周期T≤
;
即
<
, ω>100π , ω>314.2,由于ω为正整数,故ω的最小值为315.
| 1 |
| 60 |
| 1 |
| 300 |
| 1 |
| 50 |
| 2π |
| ω |
| 2π |
| T |
当t=-
| 1 |
| 300 |
| 1 |
| 300 |
| π |
| 3 |
故图象的解析式为:I=300sin(100πt+
| π |
| 3 |
(2)由 2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| k |
| 50 |
| 1 |
| 600 |
| k |
| 50 |
| 7 |
| 600 |
故函数的减区间为 [
| k |
| 50 |
| 1 |
| 600 |
| k |
| 50 |
| 7 |
| 600 |
(3)要使t在任意一段
| 1 |
| 50 |
| 1 |
| 50 |
即
| 2π |
| ω |
| 1 |
| 50 |
点评:本题考查由 y=Asin(ωx+∅)的部分图象求函数的解析式得方法,正弦函数的单调区间,以及参数的几何意义,
求出函数的解析式是解题的突破口.
求出函数的解析式是解题的突破口.

练习册系列答案
相关题目
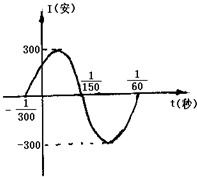 如图,表示电流强度I与时间t的关系式I=Asin(ωt+φ)(A>0,ω>0),在一个周期内的图象
如图,表示电流强度I与时间t的关系式I=Asin(ωt+φ)(A>0,ω>0),在一个周期内的图象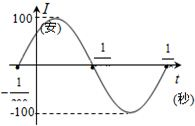 如图,表示电流强度I与时间t的函数关系式I=Asin(ωt+?)
如图,表示电流强度I与时间t的函数关系式I=Asin(ωt+?)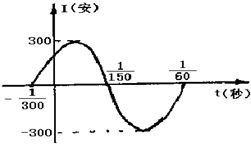 如图电流强度I与时间t的关系式
如图电流强度I与时间t的关系式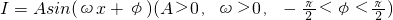 在一个周期内的图象;
在一个周期内的图象;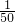 秒的时间内I能同时取得最大值和最小值,求正整数ω的最小值.
秒的时间内I能同时取得最大值和最小值,求正整数ω的最小值.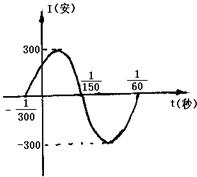 如图,表示电流强度I与时间t的关系式I=Asin(ωt+φ)(A>0,ω>0),在一个周期内的图象
如图,表示电流强度I与时间t的关系式I=Asin(ωt+φ)(A>0,ω>0),在一个周期内的图象 秒的时内I能同时取最大值|A|和最小值-|A|,那么正整数ω的最小值为多少?
秒的时内I能同时取最大值|A|和最小值-|A|,那么正整数ω的最小值为多少?