题目内容
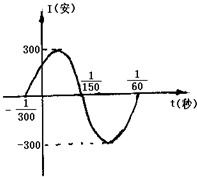 如图,表示电流强度I与时间t的关系式I=Asin(ωt+φ)(A>0,ω>0),在一个周期内的图象
如图,表示电流强度I与时间t的关系式I=Asin(ωt+φ)(A>0,ω>0),在一个周期内的图象(1)试根据图象写出I=Asin(ωt+φ)的解析式;
(2)为了使I=Asin(ωt+φ)中t在任意一段
| 1 | 100 |
分析:(1)试根据图象,直接得出A,T,然后利用周期公式求出ω,(-
,0)满足I=Asin(ωt+φ),代入A,ω,即可求出φ,写出I=Asin(ωt+φ)的解析式;
(2)使I=Asin(ωt+φ)中t在任意一段
秒的时内I能同时取最大值|A|和最小值-|A|,必须有周期T<
,得到关于ω的不等式
即可求出正整数ω的最小值.
| 1 |
| 300 |
(2)使I=Asin(ωt+φ)中t在任意一段
| 1 |
| 100 |
| 1 |
| 100 |
即可求出正整数ω的最小值.
解答:解:(1)由图可知:A=300,周期T=
-(-
)=
∴
=T?ω=
=100π
当t=-
时ωt+?=0,即?=-ωt=-100π•(-
)=
故图象的解析式为:I=300sin(100πt+
)
(2)要使t在任意一段
秒能取得最大值和最小值,必须使得周期T<
即
<
?ω>200π?ω>628.3
由于ω为正整数,故ω的最小值为:629
| 1 |
| 60 |
| 1 |
| 300 |
| 1 |
| 50 |
∴
| 2π |
| ω |
| 2π |
| T |
当t=-
| 1 |
| 300 |
| 1 |
| 300 |
| π |
| 3 |
故图象的解析式为:I=300sin(100πt+
| π |
| 3 |
(2)要使t在任意一段
| 1 |
| 100 |
| 1 |
| 100 |
即
| 2π |
| ω |
| 1 |
| 100 |
由于ω为正整数,故ω的最小值为:629
点评:本题是中档题,考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查学生视图能力,分析问题解决问题的能力,明确要使t在任意一段
秒能取得最大值和最小值,必须使得周期T<
,是解好本题的关键.
| 1 |
| 100 |
| 1 |
| 100 |

练习册系列答案
相关题目
(本小题满分14分)
如图,表示电流强度I与时间t的关系式![]() 在一个周期内的图象
在一个周期内的图象
⑴试根据图象写出![]() 的解析式;
的解析式;
|
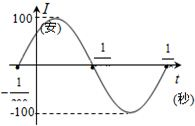 如图,表示电流强度I与时间t的函数关系式I=Asin(ωt+?)
如图,表示电流强度I与时间t的函数关系式I=Asin(ωt+?)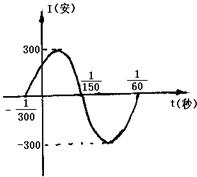 如图,表示电流强度I与时间t的关系式I=Asin(ωt+φ)(A>0,ω>0),在一个周期内的图象
如图,表示电流强度I与时间t的关系式I=Asin(ωt+φ)(A>0,ω>0),在一个周期内的图象 秒的时内I能同时取最大值|A|和最小值-|A|,那么正整数ω的最小值为多少?
秒的时内I能同时取最大值|A|和最小值-|A|,那么正整数ω的最小值为多少?
