题目内容
已知f(x)=3x,并且f(a+2)=18,g(x)=3ax-4x的定义域为[-1,1].
(1)求函数g(x)的解析式;
(2)判断g(x)的单调性;
(3)若方程g(x)=m有解,求m的取值范围.
(1)因为f(a+2)=18,f(x)=3x,
所以3a+2=18⇒3a=2,
所以g(x)=(3a)x-4x=2x-4x,x∈[-1,1].
(2)g(x)=-(2x)2+2x=-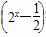 2+
2+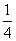 .
.
当x∈[-1,1]时,2x∈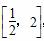 ,
,
令t=2x,所以y=-t2+t=-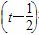 2+
2+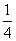 .
.
故当t∈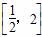 时,y=-t2+t=-
时,y=-t2+t=-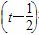 2+
2+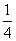 是减少的,
是减少的,
又t=2x在[-1,1]上是增加的,
所以g(x)在[-1,1]上是减少的.
(3)因为方程g(x)=m有解,即m=2x-4x在[-1,1]内有解.由(2)知g(x)=2x-4x在[-1,1]上是减少的,
所以-2≤m≤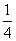 ,
,
故m的取值范围是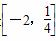 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
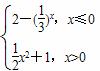 的图象恰好有3个不同的公共点,则实数m的取值范围是( )
的图象恰好有3个不同的公共点,则实数m的取值范围是( )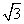 ,4) B.(
,4) B.(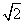 ,+∞)
,+∞) ;当x<4时,f(x)=f(x+1),则f(2+log23)=( )
;当x<4时,f(x)=f(x+1),则f(2+log23)=( ) B.
B.
 D.
D.
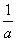 ,b) B.(10a,1-b)
,b) B.(10a,1-b)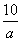 ,b+1) D.(a2,2b)
,b+1) D.(a2,2b)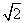 f(x)的定义域是________.
f(x)的定义域是________.