题目内容
定义在R上的函数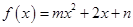 的值域是
的值域是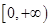 ,又对满足前面要求的任意实数
,又对满足前面要求的任意实数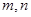 都有不等式
都有不等式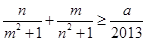 恒成立,则实数
恒成立,则实数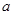 的最大值为
的最大值为
| A. 2013 | B. 1 | C. | D.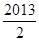 |
A
解析试题分析:函数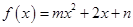 的值域是
的值域是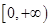
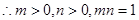 ,
,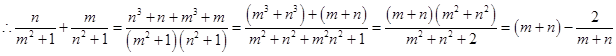
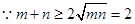 ,设
,设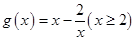 ,
,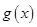 是增函数,最小值为
是增函数,最小值为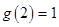
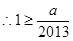 恒成立
恒成立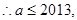 ,最大值2013
,最大值2013
考点:函数求最值及不等式性质
点评:本题主要应用的知识点有:二次函数求最值,均值不等式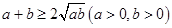 求最值,利用函数单调性求最值,综合性较强,有一定难度
求最值,利用函数单调性求最值,综合性较强,有一定难度

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
函数 的零点个数是
的零点个数是
| A.0 | B.1 |
| C.2 | D.3 |
若定义运算: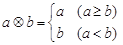 ,例如
,例如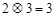 ,则下列等式不能成立的是( )
,则下列等式不能成立的是( )
A.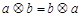 | B.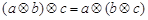 |
C.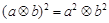 | D.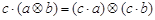 ( (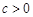 ) ) |
在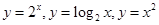 ,这三个函数中,当
,这三个函数中,当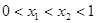 时,
时,
使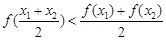 恒成立的函数的个数是( )
恒成立的函数的个数是( )
A. 个 个 | B. 个 个 | C.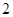 个 个 | D.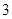 个 个 |
已知函数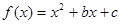 ,其中
,其中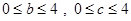 ,记函数
,记函数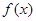 满足条件:
满足条件: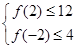 为事件
为事件 ,则事件
,则事件 发生的概率为( )
发生的概率为( )
A.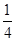 | B. | C.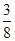 | D.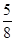 |
函数 的单调递减区间是( )
的单调递减区间是( )
A. | B. | C. | D. |
若函数 在区间
在区间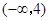 上是增函数,则有( )
上是增函数,则有( )
A. | B.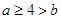 | C.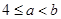 | D. |
下列函数中,既是偶函数又在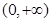 单调递增的函数是( )
单调递增的函数是( )
A.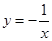 | B.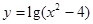 | C.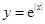 | D.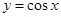 |
已知函数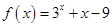 的零点为
的零点为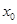 , 则
, 则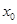 所在区间为( )
所在区间为( )
A. | B.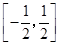 | C.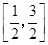 | D.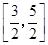 |