题目内容
函数 的单调递减区间是( )
的单调递减区间是( )
A. | B. | C. | D. |
C
解析试题分析:函数 的定义域为(0,+
的定义域为(0,+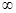 )。
)。
由 =0得,
=0得, ,在区间
,在区间 ,
, <0,函数为减函数,故选C。
<0,函数为减函数,故选C。
考点:本题主要考查利用导数研究函数的单调性。
点评:简单题,在某区间,导函数值非负,则函数为增函数;导函数值非正,则函数为减函数。

练习册系列答案
相关题目
函数 在区间
在区间 上( )
上( )
| A.没有零点 | B.只有一个零点 | C.有两个零点 | D.以上选项都错误 |
已知 为定义在
为定义在 上的可导函数,且
上的可导函数,且
 对于任意
对于任意 恒成立,则( )
恒成立,则( )
A. , , |
B. , , |
C. , , |
D. , , |
把函数 的图像向左平移
的图像向左平移 个单位,所得图像的解析式是( )
个单位,所得图像的解析式是( )
A. | B. |
C. | D. |
定义在R上的函数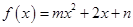 的值域是
的值域是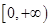 ,又对满足前面要求的任意实数
,又对满足前面要求的任意实数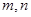 都有不等式
都有不等式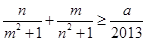 恒成立,则实数
恒成立,则实数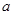 的最大值为
的最大值为
| A. 2013 | B. 1 | C. | D.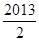 |
已知函数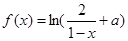 (
( 为常数)是奇函数,则实数
为常数)是奇函数,则实数 为( )
为( )
| A.1 | B.—3 | C.3 | D.—1 |
若 ,则
,则 的大小关系
的大小关系
A. | B. |
C. | D. |
当 时,函数
时,函数 取得最小值,则函数
取得最小值,则函数 是( )
是( )
A.奇函数且图像关于点 对称 对称 |
B.偶函数且图像关于点 对称 对称 |
C.奇函数且图像关于直线 对称 对称 |
D.偶函数且图像关于点 对称 对称 |
设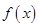 是定义在
是定义在 上以2为周期的偶函数,已知
上以2为周期的偶函数,已知 ,
,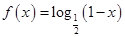 ,则函数
,则函数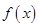 在
在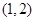 上( )
上( )
A.是增函数且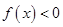 | B.是增函数且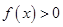 |
C.是减函数且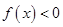 | D.是减函数且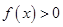 |