题目内容
设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x)=f(x+4),且当x∈[-2,0]时,f(x)=(
)x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围为 .
| 1 |
| 2 |
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:先利用已知f(x)是定义在R上的偶函数求出在区间[0,2]上的解析式,再利用周期性f(x)=f(x+4)求出函数f(x)在区间[2,4]上的解析式,然后在画出图象,进而求出a的取值范围.
解答:
解:设x∈[0,2],则-x∈[-2,0],∴f(-x)=(
)-x-1=2x-1,
∵f(x)是定义在R上的偶函数,∴f(x)=f(-x)=2x-1.
∵对任意x∈R,都有f(x)=f(x+4),
∴当x∈[2,4]时,(x-4)∈[-2,0],∴f(x)=f(x-4)=xx-4-1;
当x∈[4,6]时,(x-4)∈[0,2],∴f(x)=f(x-4)=2x-4-1.
∵若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有三个不同的实数根,
∴函数y=f(x)与函数y=loga(x+2)在区间(-2,6]上恰有三个交点,
通过画图可知:恰有三个交点的条件是
,解得 2
<a<2,
即
<a<2,因此所求的a的取值范围为(
,2).
故答案为:(
,2).
| 1 |
| 2 |
∵f(x)是定义在R上的偶函数,∴f(x)=f(-x)=2x-1.
∵对任意x∈R,都有f(x)=f(x+4),
∴当x∈[2,4]时,(x-4)∈[-2,0],∴f(x)=f(x-4)=xx-4-1;
当x∈[4,6]时,(x-4)∈[0,2],∴f(x)=f(x-4)=2x-4-1.
∵若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有三个不同的实数根,
∴函数y=f(x)与函数y=loga(x+2)在区间(-2,6]上恰有三个交点,
通过画图可知:恰有三个交点的条件是
|
| 2 |
| 3 |
即
| 3 | 4 |
| 3 | 4 |
故答案为:(
| 3 | 4 |
点评:本题综合考查了函数的奇偶性、周期性、函数的交点及方程的根,熟练掌握函数的性质及数形结合是解决问题的关键.

练习册系列答案
相关题目
某电视台在娱乐频道节目播放中,每小时播放广告20分钟,那么随机打开电视机观看这个频道看到广告的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
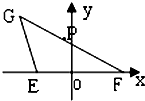 已知E、F是x轴上的点,坐标原点O为线段EF的中点,G、P是坐标平面上的动点,点P在线段FG上,|
已知E、F是x轴上的点,坐标原点O为线段EF的中点,G、P是坐标平面上的动点,点P在线段FG上,|