题目内容
已知二次函数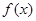 的对称轴方程为:
的对称轴方程为: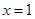 ,设向量
,设向量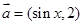 ,
,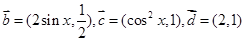 .
.
(1)分别求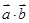 和
和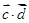 的取值范围;
的取值范围;
(2)当 时,求不等式
时,求不等式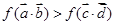 的解集.
的解集.
(1)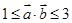 ,
, ;(2)当
;(2)当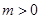 时,不等式的解集为
时,不等式的解集为 ;当
;当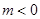 时,不等式的解集为
时,不等式的解集为 .
.
解析试题分析:(1)先由平面向量数量积的坐标运算公式计算出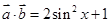 ,
,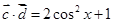 ,然后根据正余弦函数的值域,即可得到
,然后根据正余弦函数的值域,即可得到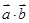 和
和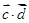 的取值范围;(2)由(1)所求得的范围,与题中条件二次函数
的取值范围;(2)由(1)所求得的范围,与题中条件二次函数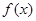 的对称轴方程为:
的对称轴方程为: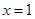 ,分
,分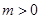 、
、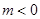 两类考虑函数
两类考虑函数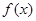 在
在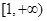 的单调性,进而将不等式
的单调性,进而将不等式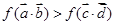 转化为
转化为 、
、 两种情况进行求解,最后结合所给
两种情况进行求解,最后结合所给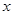 的范围与正余弦函数的性质可得原不等式的解集.
的范围与正余弦函数的性质可得原不等式的解集.
试题解析:(1)依题意可得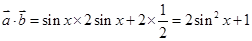 ,
,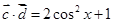
因为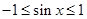 ,
,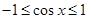 ,所以
,所以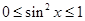 ,
,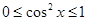 ,所以
,所以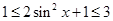 ,
,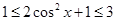 即
即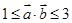 ,
,
(2)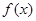 图像关于
图像关于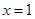 对称
对称
当二次项系数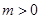 时,
时,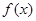 在
在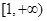 内单调递增,由
内单调递增,由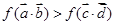 得到
得到 即
即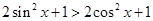 即
即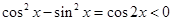
又因为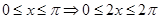
所以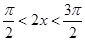 即
即
当二次项系数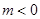 时,
时,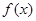 在
在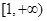 内单调递减
内单调递减
由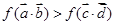 得到
得到 即
即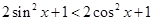 即
即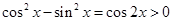
又因为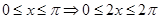
所以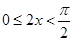 或
或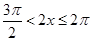 即
即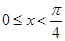 或
或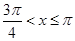
综上,当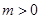 时不等式的解集为
时不等式的解集为 ;当
;当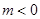 时不等式的解集为
时不等式的解集为 .
.
考点:1.平面向量的坐标运算;2.二次函数的图像与性质;3.平面向量的数量积.

练习册系列答案
相关题目
 中,动点
中,动点 到两点
到两点 、
、 的距离之和等于4.设点
的距离之和等于4.设点 .
.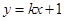 与
与 、
、 两点,若
两点,若 ,求
,求 的值.
的值. 的准线上,且椭圆C过点
的准线上,且椭圆C过点 .
. 作直线
作直线 与椭圆C相交于E,F两点,直线AE,AF与直线
与椭圆C相交于E,F两点,直线AE,AF与直线 分别交于不同的两点M,N,求
分别交于不同的两点M,N,求 的取值范围.
的取值范围.
 ,
,
 ,
,  的值。
的值。 为何值时,
为何值时,
 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?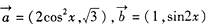 ,函数
,函数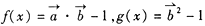
 ,
, .
. ,
, ,且
,且 ,求
,求 ;
; ,求
,求 的取值范围.
的取值范围. 中,满足:
中,满足: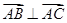 ,
,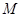 是
是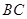 的中点.
的中点.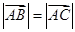 ,求向量
,求向量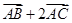 与向量
与向量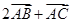 的夹角的余弦值;
的夹角的余弦值; 是
是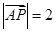 ,且
,且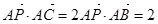 ,求
,求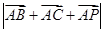 的最小值.
的最小值.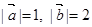 ,且
,且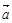 与
与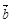 的夹角为120°.
的夹角为120°.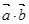 ; (2)
; (2) 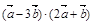 ; (3)
; (3) 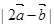 .
.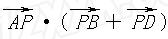 的取值范围是________.
的取值范围是________.