题目内容
等差数列{an}的前n项和为Sn,已知(a2-1)3+2011(a2-1)=
,(a2010-1)3+2011(a2010-1)=-
,则S2011等于( )
| ||
| 2 |
| ||
| 2 |
| A、0 | ||
| B、2011 | ||
| C、4022 | ||
D、2011
|
考点:等差数列的性质
专题:等差数列与等比数列
分析:两个等式相加,然后因式分解,提取公因式得到a2+a2010的值,利用等差数列的性质及数列的前n项和公式可得.
解答:
解:已知两式相加可得(a2-1)3+2011(a2-1)+(a2010-1)3+2011(a2010-1)=0,
整理可得(a2-1+a2010-1)[(a2-1)2-(a2-1)(a2010-1)+(a2010-1)2]+2011(a2-1+a2010-1)=0,
∴a2-1+a2010-1=0,即a2+a2010=2,
∵{an}为等差数列,前n项和为Sn,
∴S2011=
=
=2011
故选:B.
整理可得(a2-1+a2010-1)[(a2-1)2-(a2-1)(a2010-1)+(a2010-1)2]+2011(a2-1+a2010-1)=0,
∴a2-1+a2010-1=0,即a2+a2010=2,
∵{an}为等差数列,前n项和为Sn,
∴S2011=
| 2011(a1+a2011) |
| 2 |
| 2011(a2+a2010) |
| 2 |
故选:B.
点评:本题主查等差数列的前n项和,求出a2+a2010=2是解决本题的关键,属基础题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
函数y=2sin2x的图象的一个对称中心是( )
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
函数y=loga(2x-3)+2的图象恒过定点P,P在指数函数f(x)的图象上,则f(-1)的值为( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
高三年级有5个班级参加学校运动会100米跑决赛,共有5个跑道,若在安排比赛赛道时不将甲班安排在第一及第二赛道上,且甲班和乙班不相邻,则不同的安排方法有( )
| A、24种 | B、30种 |
| C、36种 | D、42种 |
已知函数f(x)=
(et-e-t)dt,则不等式f(loga2)+f(loga
)≤2f(1)的解集为( )
| ∫ | x 0 |
| 1 |
| 2 |
A、(0,
| ||
| B、[2,+∞) | ||
C、[
| ||
D、(0,
|
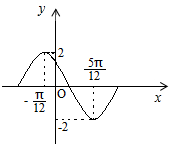 如图是函数y=Asin(ωx+φ)在一个周期内的图象,如果A>0,ω>0,0<φ<π,则此函数的解析式为
如图是函数y=Asin(ωx+φ)在一个周期内的图象,如果A>0,ω>0,0<φ<π,则此函数的解析式为