题目内容
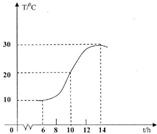 某地一天从6~14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,则这段曲线得函数解析式为( )
某地一天从6~14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,则这段曲线得函数解析式为( )A、y=10sin(
| ||||
B、y=10sin(
| ||||
C、y=10sin(
| ||||
D、y=10sin(
|
分析:已知函数图象求函数y=Asin(ωx+φ)(A>0,ω>0)的解析式时,常用的解题方法是待定系数法,由图中的最大值或最小值确定A,由周期确定ω,由适合解析式的点的坐标来确定φ.将图中数据点代入即可求出相应系数,进而得到函数的解析式.
解答:解:由函数图象可知,
函数的最大值M为30,最小值m为10,
周期为2×(14-6)=16,
且过(6,10)点
则2A=30-10=20,∴A=10
2B=30+10=40,∴B=20
T=16=
,∴ω=
将(6,10)点代入易得φ=
故函数的解析式为:y=10sin(
x+
π)+20,x∈[6,14]
故选A
函数的最大值M为30,最小值m为10,
周期为2×(14-6)=16,
且过(6,10)点
则2A=30-10=20,∴A=10
2B=30+10=40,∴B=20
T=16=
| 2π |
| ω |
| π |
| 8 |
将(6,10)点代入易得φ=
| 3π |
| 4 |
故函数的解析式为:y=10sin(
| π |
| 8 |
| 3 |
| 4 |
故选A
点评:由函数图象求函数y=Asin(ωx+φ)+B(A>0,ω>0)的解析式时,由图中的最大值或最小值确定A、B,由周期确定ω,由适合解析式的点的坐标来确定φ,但由图象求得的y=Asin(ωx+φ)(A>0,ω>0)的解析式一般不唯一,只有限定φ的取值范围,才能得出唯一解,否则φ的值不确定,解析式也就不唯一.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
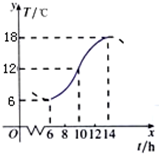 如图所示,某地一天从6~14时的温度变化曲线近似满足函数:f(x)=Asin(ωx+φ)+b,x∈[6,14],则这段曲线的解析式为( )
如图所示,某地一天从6~14时的温度变化曲线近似满足函数:f(x)=Asin(ωx+φ)+b,x∈[6,14],则这段曲线的解析式为( )A、f(x)=12sin(
| ||||
B、f(x)=6sin(
| ||||
C、f(x)=6sin(
| ||||
D、f(x)=12sin(
|
 如图,某地一天从6~14时的温度变化曲线近似满足函数:y=Asin(ωx+φ)+b,则A、ω、φ、b分别是( )
如图,某地一天从6~14时的温度变化曲线近似满足函数:y=Asin(ωx+φ)+b,则A、ω、φ、b分别是( )A、A=10、ω=
| ||||
B、A=20、ω=
| ||||
C、A=30、ω=
| ||||
D、A=10、ω=
|
 (2011•佛山二模)如图,某地一天从6~14时的温度变化曲线近似满足函数:y=Asin(ωx+φ)+B.则中午12点时最接近的温度为( )
(2011•佛山二模)如图,某地一天从6~14时的温度变化曲线近似满足函数:y=Asin(ωx+φ)+B.则中午12点时最接近的温度为( ) 如图所示,某地一天从6时至14时的温度变化曲线近似满足y=Asin(ωx+φ)+b.
如图所示,某地一天从6时至14时的温度变化曲线近似满足y=Asin(ωx+φ)+b.