题目内容
如图,函数y=2sin(πx+ψ),x∈R(其中0≤ψ≤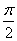 )的图象与y轴交于点(0,1),
)的图象与y轴交于点(0,1),
(Ⅰ)求ψ的值;
(Ⅱ)设P是图象上的最高点,M,N是图象与x轴的交点,求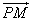 与
与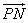 的夹角。
的夹角。
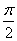 )的图象与y轴交于点(0,1),
)的图象与y轴交于点(0,1),(Ⅰ)求ψ的值;
(Ⅱ)设P是图象上的最高点,M,N是图象与x轴的交点,求
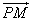 与
与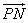 的夹角。
的夹角。 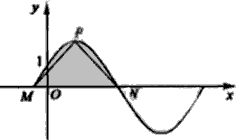
解:(Ⅰ)因为函数图象过点(0,1),
所以2sinψ=1,即sinψ=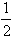 ,
,
因为0≤ψ≤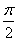 ,所以ψ=
,所以ψ=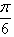 ;
;
(Ⅱ)由函数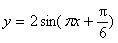 及其图象,得
及其图象,得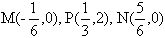 ,
,
所以,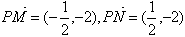 ,
,
从而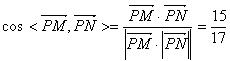 ,
,
故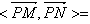
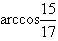 。
。
所以2sinψ=1,即sinψ=
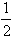 ,
,因为0≤ψ≤
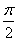 ,所以ψ=
,所以ψ=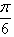 ;
;(Ⅱ)由函数
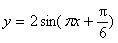 及其图象,得
及其图象,得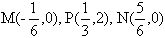 ,
,所以,
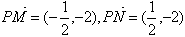 ,
,从而
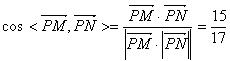 ,
,故
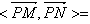
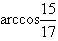 。
。
练习册系列答案
相关题目
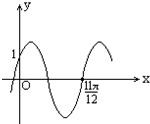
已知如图是函数y=2sin(ωx+φ)(|φ|<
)的图象,那么( )
| π |
| 2 |

A、?=
| ||||
B、?=
| ||||
C、?=2,φ=
| ||||
D、?=2,φ=-
|
 如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤
如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤ 已知如图是函数y=2sin(ωx+φ)(|φ|<
已知如图是函数y=2sin(ωx+φ)(|φ|< 如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤
如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤ 如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤
如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤