题目内容
10.某三棱锥的三视图如图所示,该三棱锥的四个面的面积中,最大的面积是( )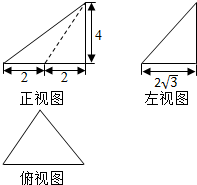
| A. | 4$\sqrt{3}$ | B. | 8 $\sqrt{3}$ | C. | 4$\sqrt{7}$ | D. | 8 |
分析 根据三视图分析出几何体的图形,利用三视图中的数据求出四个面的面积中的最大值.
解答  解:根据几何体的三视图知,该几何体底面是边长为4的正三角形,高为4的三棱锥,
解:根据几何体的三视图知,该几何体底面是边长为4的正三角形,高为4的三棱锥,
且侧棱垂直于底面三角形的一个顶点,如图所示;
则两个垂直底面的侧面面积为S△PAC=S△PAB=$\frac{1}{2}$×4×4=8;
底面面积为S△ABC=$\frac{1}{2}$×42×sin60°=4$\sqrt{3}$;
另一个侧面的面积为S△PBC=$\frac{1}{2}$×4×$\sqrt{{4}^{2}{+4}^{2}{-2}^{2}}$=4$\sqrt{7}$;
所以四个面中面积的最大值为4$\sqrt{7}$.
故选:C.
点评 本题考查了利用三视图求几何体各个面的面积的应用问题,也考查了空间想象能力与计算能力,是基础题.

练习册系列答案
相关题目
18.在5件产品中,有4件正品,从中任取2件,2件都是正品的概率是( )
| A. | $\frac{4}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
15.下列语句不是命题的是( )
| A. | 祁阳一中是一所一流名校 | |
| B. | 如果这道题做不到,那么这次考试成绩不理想 | |
| C. | ?x∈R,使得lnx0<0 | |
| D. | 画一个椭圆 |
2.过抛物线y2=$\frac{1}{2}$x的焦点作倾斜角为30°的直线与抛物线交于P、Q两点,则|PQ|=( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | 1 |
19. 对某杂志社一个月内每天收到的稿件数量进行了统计,得到样本的茎叶图(如图),则该样本的中位数、众数分别为( )
对某杂志社一个月内每天收到的稿件数量进行了统计,得到样本的茎叶图(如图),则该样本的中位数、众数分别为( )
 对某杂志社一个月内每天收到的稿件数量进行了统计,得到样本的茎叶图(如图),则该样本的中位数、众数分别为( )
对某杂志社一个月内每天收到的稿件数量进行了统计,得到样本的茎叶图(如图),则该样本的中位数、众数分别为( )| A. | 47、45 | B. | 45、47 | C. | 46、45 | D. | 45、46 |