题目内容
5.已知函数f(x)=ax2+bx+c(a>0且bc≠0).(Ⅰ)若|f(0)|=|f(1)|=|f(-1)|=1,试求f(x)的解析式;
(Ⅱ)令g(x)=2ax+b,若g(1)=0,又f(x)的图象在x轴上截得的弦的长度为l,且0<l≤2,试比较b、c的大小.
分析 (Ⅰ)由已知可得(a+b+c)2=(a-b+c)2,得4b(a+c)=0,|c|=1,结合条件即可得到a,b,c,进而得到f(x)的解析式;
(Ⅱ)g(1)=0,可得2a+b=0,设方程f(x)=0的两根为x1,x2,运用韦达定理,以及弦长公式,求得$0≤\frac{c}{a}<1$.进而得到b,c的大小.
解答 解:(Ⅰ)由已知|f(0)|=|f(1)|=|f(-1)|=1,
有|a+b+c|=|a-b+c|⇒(a+b+c)2=(a-b+c)2,得4b(a+c)=0.
∵bc≠0,∴b≠0,∴a+c=0,由a>0知,c<0,
∵|c|=1,∴c=-1.
则a=1,b=±1.
∴f(x)=x2+x-1或f(x)=x2-x-1.
(Ⅱ)g(x)=2ax+b,由g(1)=0且a>0,
知2a+b=0,b<0且a>0,
设方程f(x)=0的两根为x1,x2,
则${x_1}+{x_2}=-\frac{b}{a}=2$,${x_1}{x_2}=\frac{c}{a}$,
∴$|{x_1}-{x_2}|=\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}=\sqrt{4-4•\frac{c}{a}}$,
由已知0<|x1-x2|≤2,∴$0≤\frac{c}{a}<1$.
又∵a>0,bc≠0,
∴c>0,又b<0,
∴c>0>b.
点评 本题考查二次函数的解析式的求法,注意运用待定系数法,考查两数大小的比较,注意运用韦达定理和不等式的性质,属于中档题.

练习册系列答案
相关题目
16.设f(x)是R上的奇函数,且当x∈(0,+∞)时,f(x)=x2-1,则当x∈(-∞,0)时,f(x)=( )
| A. | x2+1 | B. | x2-1 | C. | -x2+1 | D. | -x2-1 |
20.用系统抽样法从140名学生中抽取容量为20的样本,将140名学生从1~140编号,按编号顺序平均分成20组(1~7号,8~14号,…,134~140号).若第16组抽出的号码是110,则第1组抽出的号码是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
10.某三棱锥的三视图如图所示,该三棱锥的四个面的面积中,最大的面积是( )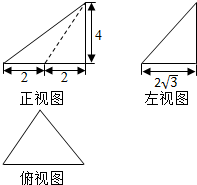

| A. | 4$\sqrt{3}$ | B. | 8 $\sqrt{3}$ | C. | 4$\sqrt{7}$ | D. | 8 |
15.已知函数f(x)=excosx,则函数f(x)在点(0,f(0))处的切线方程为( )
| A. | y=1 | B. | x-y+1=0 | C. | x+y+1=0 | D. | x-y=0 |